- #1
crick
- 43
- 4
Suppose that I use a prism (vertex angle ##\alpha##) spectroscope to analyze a beam of visible light from a mercury lamp (different wavelenghts) and I want the determine the refraction index of the prism using the minmum deviation angles ##D_{min}##
$$n(\lambda)=\frac{\mathrm{sin}(\frac{D_{min}(\lambda)+\alpha }{2})}{\mathrm{sin}\frac{\alpha}{2}}$$
##D_{min}## depends on ##\lambda## and so does ##n##.
Nevertheless suppose that, even if I want to find experimentally ##D_{min}## for all the spectral lines that I see in the spectroscope, I want to do the setting of the prism for minmum deviation condition only for the two extreme ones, say a violet and a red and then try to extimate the values of ##D_{min}## for other wavelenghts from these two. (I know that this is not theoretically correct).
Therefore I set the prism in the condition of minimum deviation for red and then I measure the angle of deviation ##D## for all the other ##\lambda##s (i'll take, for example, the yellow one) and then I repeat the same procedure but setting the condition of minimum deviation for violet.
My question is: should I expect that $$D_{yellow_{\mathrm{minmum \, deviation \, condition \,for \,RED}}}<D_{yellow_{\mathrm{minmum \, deviation \, condition \,for \,VIOLET}}}$$
or the opposite? Or nothing can be said?
More generally how does ##D_{yellow}## vary as a function of the wavelenght (or frequency) for which the minimum deviation condition is set in the spectroscope?
Alternatevely, called ##i## the angle of incidence on the prism of the beam, what should I expect for the relation between ##D_{min}##, ##\lambda## and ##i##?
I know that $$D(i)=i -\alpha +\mathrm{arcsin}(\mathrm{sin}\sqrt{n^2+\mathrm{sin }^2 i}-\mathrm{cos} \alpha \,\,\,\mathrm{sin}i)$$
Which leads to something like
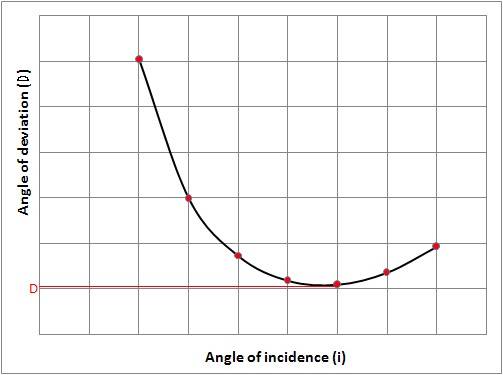
Also, under minimum deviation condition, ##D_{min}=2i-\alpha##.
But what is the relation ##D_{min}(\lambda)##? As far as I understood it should be decreasing (therefore ##D_{min}(f)## is increasing), but i do not think that it is a direct proportionality (correct?)
If what I said is correct, then suppose to plot ##D_{yellow_{\mathrm{minmum \, deviation \, condition \,for \,RED}}}## and ##D_{yellow_{\mathrm{minmum \, deviation \, condition \,for \,VIOLET}}}## as a function of the frequencies of red and violet. Should I expect to have a curve of tendency as the one in picture?
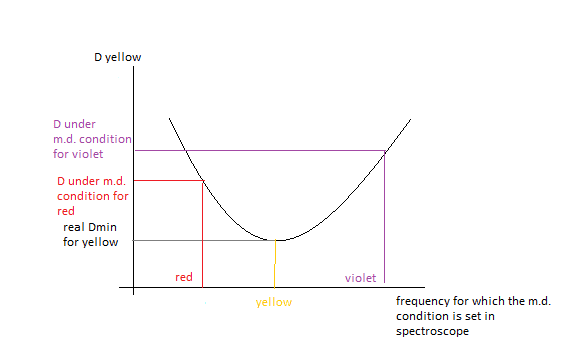
If this is the case then I cannot say which between red or violet would give the higher deviation for yellow, unless there is a way to get the function that describes the behaviour in the above graph, is there one?
Any suggestion on the topic or reference on where to find information about this is highly appreciated
$$n(\lambda)=\frac{\mathrm{sin}(\frac{D_{min}(\lambda)+\alpha }{2})}{\mathrm{sin}\frac{\alpha}{2}}$$
##D_{min}## depends on ##\lambda## and so does ##n##.
Nevertheless suppose that, even if I want to find experimentally ##D_{min}## for all the spectral lines that I see in the spectroscope, I want to do the setting of the prism for minmum deviation condition only for the two extreme ones, say a violet and a red and then try to extimate the values of ##D_{min}## for other wavelenghts from these two. (I know that this is not theoretically correct).
Therefore I set the prism in the condition of minimum deviation for red and then I measure the angle of deviation ##D## for all the other ##\lambda##s (i'll take, for example, the yellow one) and then I repeat the same procedure but setting the condition of minimum deviation for violet.
My question is: should I expect that $$D_{yellow_{\mathrm{minmum \, deviation \, condition \,for \,RED}}}<D_{yellow_{\mathrm{minmum \, deviation \, condition \,for \,VIOLET}}}$$
or the opposite? Or nothing can be said?
More generally how does ##D_{yellow}## vary as a function of the wavelenght (or frequency) for which the minimum deviation condition is set in the spectroscope?
Alternatevely, called ##i## the angle of incidence on the prism of the beam, what should I expect for the relation between ##D_{min}##, ##\lambda## and ##i##?
I know that $$D(i)=i -\alpha +\mathrm{arcsin}(\mathrm{sin}\sqrt{n^2+\mathrm{sin }^2 i}-\mathrm{cos} \alpha \,\,\,\mathrm{sin}i)$$
Which leads to something like
Also, under minimum deviation condition, ##D_{min}=2i-\alpha##.
But what is the relation ##D_{min}(\lambda)##? As far as I understood it should be decreasing (therefore ##D_{min}(f)## is increasing), but i do not think that it is a direct proportionality (correct?)
If what I said is correct, then suppose to plot ##D_{yellow_{\mathrm{minmum \, deviation \, condition \,for \,RED}}}## and ##D_{yellow_{\mathrm{minmum \, deviation \, condition \,for \,VIOLET}}}## as a function of the frequencies of red and violet. Should I expect to have a curve of tendency as the one in picture?
If this is the case then I cannot say which between red or violet would give the higher deviation for yellow, unless there is a way to get the function that describes the behaviour in the above graph, is there one?
Any suggestion on the topic or reference on where to find information about this is highly appreciated