Minimum Spanning Tree of a Graph Solutions

[whoareyou]

I recently wrote a program that implements a slightly modified version of Prim's Algorithm to find a minimal spanning tree and it seems to work correctly. However, I am doubtful because my prof claims that this certain tree has more than 1 solution but my program gives only one solution. Note that a different solution means that different edges are used to visit every node. Using the same edges in a different order is not a different solution. Can someone please confirm this:

GRAPH:

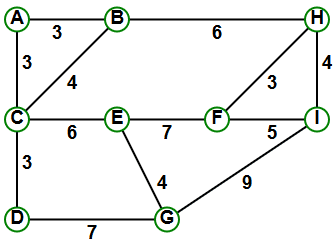
SOLUTIONS (in each case, all the links are the same, ∴ only 1 solution):

A -> B: 3
A -> C: 3
C -> D: 3
B -> H: 6
H -> F: 3
H -> I: 4
C -> E: 6
E -> G: 4

TOTAL DISTANCE: 32

B -> A: 3
A -> C: 3
C -> D: 3
B -> H: 6
H -> F: 3
H -> I: 4
C -> E: 6
E -> G: 4

TOTAL DISTANCE: 32

C -> A: 3
C -> D: 3
A -> B: 3
C -> E: 6
E -> G: 4
B -> H: 6
H -> F: 3
H -> I: 4

TOTAL DISTANCE: 32

D -> C: 3
C -> A: 3
A -> B: 3
C -> E: 6
E -> G: 4
B -> H: 6
H -> F: 3
H -> I: 4

TOTAL DISTANCE: 32

E -> G: 4
E -> C: 6
C -> A: 3
C -> D: 3
A -> B: 3
B -> H: 6
H -> F: 3
H -> I: 4

TOTAL DISTANCE: 32

F -> H: 3
H -> I: 4
H -> B: 6
B -> A: 3
A -> C: 3
C -> D: 3
C -> E: 6
E -> G: 4

TOTAL DISTANCE: 32

G -> E: 4
E -> C: 6
C -> A: 3
C -> D: 3
A -> B: 3
B -> H: 6
H -> F: 3
H -> I: 4

TOTAL DISTANCE: 32

H -> F: 3
H -> I: 4
H -> B: 6
B -> A: 3
A -> C: 3
C -> D: 3
C -> E: 6
E -> G: 4

TOTAL DISTANCE: 32

I -> H: 4
H -> F: 3
H -> B: 6
B -> A: 3
A -> C: 3
C -> D: 3
C -> E: 6
E -> G: 4

TOTAL DISTANCE: 32

 

[whoareyou]

bump, no one can confirm this?

 

[lewando]

To confirm that your solution is the only one, evaluate every possible configuration for total distance and connectedness. Then call your professor's bluff (you should).