Minimum Speeds for 100g Particles on Energy/Distance Graph

[Honore]

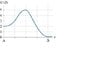
With reference to the attached "energy versus distance graph" of two particles;

a. What minimum speed (m/s) does a 100 g particle need at point A to reach point B?

b. What minimum speed (m/s) does a 100 g particle need at point B to reach point A?

Thank you.

 

[Galileo]

Use conservation of energy. First find the minimum kinetic energy needed to go from A to B, then get the speed from that.

 

[Honore]

Use conservation of energy. First find the minimum kinetic energy needed to go from A to B, then get the speed from that.

In order to find the minimum kinetic energy, I think I have to find the total work done referring to a "Force vs Distance" graph. But, how can "Force" be found from a graph which is not linear?

 

[whozum]

Work = \int F dx

Is this gravitational potential? In that case, its conservative, and you can ignore anything but the starting and ending points. You lost 2 Joules of PE to get from A to B, so you gained 2 Joules of KE.

KE = 1/2 mv^2

2 = 1/2 (100g) v^2

 

[Galileo]

In one dimension, any position dependent force is conservative (the potential (or total?) energy is already given as a function of the position).

 

[whozum]

Isnt "position dependant force" part of the definition of "conservative force"? Say there was a resistance factor such as friction, the energy wouldn't be conserved then.