- #1
deuteron
- 51
- 12
TL;DR Summary: I am missing an algebraic step in the below described three-body problem, any help is much appreciated
Consider the following setup
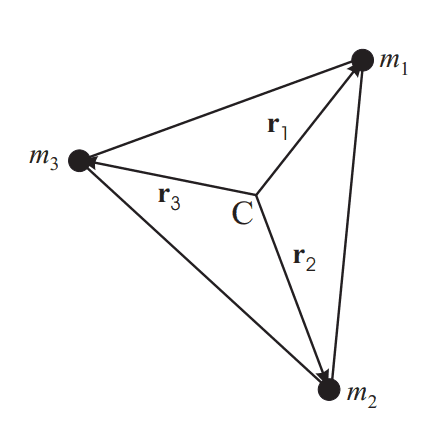
where the distance between the masses are ##d##, and they exert gravitational force on each other. We want to find the angular velocity of the rotation of such system, for which we first need to find the total force on the masses.
What I would've done is the following:
$$m_i\ddot r_i=F_i = G \frac {m_i m_j}{|\vec r_i -\vec r_j|^2} \frac {\vec r_i-\vec r_j}{|\vec r_i-\vec r_j|} +G\frac {m_i m_k}{|\vec r_i-\vec r-k|^2} \frac {\vec r_i-\vec r_k}{|\vec r_i-\vec r_k|}
\\ = G\frac {m_i m_j}{d^3}(\vec r_i-\vec r_j)+G\frac {m_i m_k}{d^3}(\vec r_i-\vec r_k)
\\ = \frac G {d^3}\ [ m_i m_j\vec r_i -m_im_j \vec r_j + m_im_k \vec r_i -m_im_k\vec r_k]
\\ = \frac G {d^3}\ [(m_im_j +m_im_k)\vec r_i -m_im_j\vec r_j +m_im_k\vec r_k]$$
But I am stuck here. In the solution of the problem, the final equation to be reached was:
$$\frac {d^2r_i}{dt^2} =\frac G{d^3} (m_i+m_j+m_k)r_i$$
I feel like I am missing a very obvious algebraic step but can't figure it out.
Consider the following setup
where the distance between the masses are ##d##, and they exert gravitational force on each other. We want to find the angular velocity of the rotation of such system, for which we first need to find the total force on the masses.
What I would've done is the following:
$$m_i\ddot r_i=F_i = G \frac {m_i m_j}{|\vec r_i -\vec r_j|^2} \frac {\vec r_i-\vec r_j}{|\vec r_i-\vec r_j|} +G\frac {m_i m_k}{|\vec r_i-\vec r-k|^2} \frac {\vec r_i-\vec r_k}{|\vec r_i-\vec r_k|}
\\ = G\frac {m_i m_j}{d^3}(\vec r_i-\vec r_j)+G\frac {m_i m_k}{d^3}(\vec r_i-\vec r_k)
\\ = \frac G {d^3}\ [ m_i m_j\vec r_i -m_im_j \vec r_j + m_im_k \vec r_i -m_im_k\vec r_k]
\\ = \frac G {d^3}\ [(m_im_j +m_im_k)\vec r_i -m_im_j\vec r_j +m_im_k\vec r_k]$$
But I am stuck here. In the solution of the problem, the final equation to be reached was:
$$\frac {d^2r_i}{dt^2} =\frac G{d^3} (m_i+m_j+m_k)r_i$$
I feel like I am missing a very obvious algebraic step but can't figure it out.
Last edited by a moderator: