Mixing with Common Drain: Mass of Salt in Two Tanks #46 Nagle

[mathcoral]

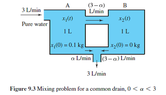
Mixing with a Common Drain. Two tanks, each holding 1 L of liquid, are connected by a pipe through which liquid flows from tank A into tank B at a rate of 3-a L/min (0<a<3). The liquid inside each tank is kept well stirred. Pure water flows into tank A at a rate of 3 L/min. Solution flows out of tank A at a L/min and out of tank B at 3-a L/min. If, initially, tank B contains no salt (only water) and tank A contains 0.1 kg of salt, determine the mass of salt in each tank at time T>=0. How does the mass of salt in tank A depend on the choice of a? What is the maximum mass of salt in tank B?Here is picture of the tank View attachment 8094

I was going to make a normal equation x'=Ax to find the eigenvectors.

I got stuck on the set up
x₁=rate in - rate out
x₁(t)=0 - (3-a)x₁(t) - ax₁(t)
x₁(t)= -3x₁(t)
The rate in is 0 because the liquid is pure water.

x₂(t) =rate in - rate out
x₂(t)= (3-a)x₁(t) - (3-a)x₂(t)

I am unsure how to put the 3 L/min coming out of from both tanks (bottom pipe).

 

[MarkFL]

I would begin with:

$$\d{x_1}{t}=-3x_1$$ where $$x_1(0)=\frac{1}{10}$$

Hence:

$$x_1(t)=\frac{e^{-3t}}{10}$$

Then:

$$\d{x_2}{t}=(3-\alpha)\left(\frac{e^{-3t}}{10}-x_2\right)$$ where $$x_2(0)=0$$

I would put the ODE into standard linear form:

$$\d{x_2}{t}+(3-\alpha)x_2=(3-\alpha)\frac{e^{-3t}}{10}$$

Our integrating factor is:

$$\mu(t)=e^{(3-\alpha)t}$$

And we get:

$$e^{(3-\alpha)t}\d{x_2}{t}+(3-\alpha)e^{(3-\alpha)t}x_2=(3-\alpha)\frac{e^{-3t}}{10}e^{(3-\alpha)t}$$

Or:

$$\frac{d}{dt}\left(e^{(3-\alpha)t}x_2\right)=(3-\alpha)\frac{e^{-\alpha t}}{10}$$

Can you proceed?

 

[mathcoral]

After integrating I got
x₂(t)=$$\frac{3-a}{10a}$$(e^at-1)e^-3t

The mass of salt in tank A does not depend on the choice of a.
Tank B depends on a.

I am unsure how to find the maximum mass for tank B.

 

[MarkFL]

After integrating I got
x₂(t)=$$\frac{3-a}{10a}$$(e^at-1)e^-3t

The mass of salt in tank A does not depend on the choice of a.
Tank B depends on a.

I am unsure how to find the maximum mass for tank B.

I got the equivalent:

$$x_2(t)=\frac{\alpha-3}{10\alpha}e^{-3t}\left(1-e^{\alpha t}\right)$$

Now, for the optimization of this function, recall we had:

$$\d{x_2}{t}=(3-\alpha)\left(\frac{e^{-3t}}{10}-x_2\right)$$

Note: We could also differentiate the function we found, but I think this will be less work. ;)

We can equate this derivative to zero to find the turning point, and substitute for $x_2$:

$$(3-\alpha)\left(\frac{e^{-3t}}{10}-\frac{\alpha-3}{10\alpha}e^{-3t}\left(1-e^{\alpha t}\right)\right)=0$$

Since we are given $0<\alpha<3$, we may divide through by $$\frac{3-\alpha}{10\alpha}$$ to obtain:

$$\alpha e^{-3t}-(\alpha-3)e^{-3t}\left(1-e^{\alpha t}\right)=0$$

Solve this for $t=t_{\max}$ and then evaluate $x_2\left(t_{\max}\right)$.

 

[mathcoral]

Setting the derivative to 0 I got t=$$\frac{ln(\frac{3}{3-a})}{a}$$

Plugging in for t in x₂(t) I got
x₂(t)=.1($$\frac{3-a}{3}$$)^3/a kg

 

[MarkFL]

Setting the derivative to 0 I got t=$$\frac{ln(\frac{3}{3-a})}{a}$$

Plugging in for t in x₂(t) I got
x₂(t)=.1($$\frac{3-a}{3}$$)^3/a kg

Yes, I get equivalent results. (Yes)

 

[I like Serena]

Hi mathcoral, welcome to MHB!

It seem to me that we still don't have the actual maximum mass of salt in tank B.
For that we need to maximize for $\alpha$ as well.
We can make it ourselves a little easier, since to achieve that maximum all liquid from tank A should go through tank B, shouldn't it?
So $\alpha = 0$.
How much salt would that make at its maximum in tank B? (Wondering)