David112234
- 105
- 3
So the moment of inertia or a ring is MR2 I don't understand why. Here is my reasoning
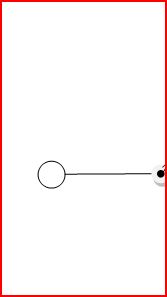
Consider this shape (the ball is a point), the moment of inertia is MR2, there I agree
but now
what happens when you add another point on the other side
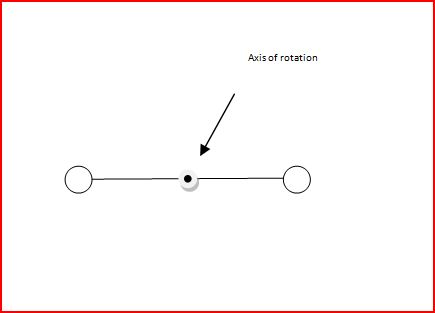
since I = ΣMR2 then this is 2MR2
What about a ring or circle, that is nothing more than a bunch of points all the same distance from the center
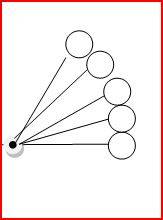
so how many points are there? The circumference
so I= πR2MR2
I know that different objects moment of inertia differ by a number in front, like 1/2 or 3/5
Why is their no number prefix for Inertia in front of the formula for a hoop/ hollow cylinder/ circle that represents its circumference? How is this even derived?
Second question, How do you represent the angular Kinetic energy of this object?
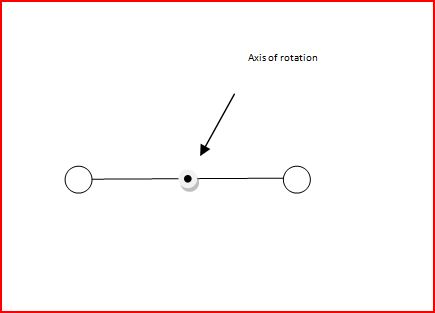 Left Point = A
Left Point = A
Right point = B
½ I ωA2 + ⅓ I ωB2
½ I ( ωA2+ωB2 )
both objects have same ω so
½ I 2ω2
Or
do I use ω to represent the angular velocity of the whole object and just keep it as
½ I ω2 with whatever I is from the previous question?
Consider this shape (the ball is a point), the moment of inertia is MR2, there I agree
but now
what happens when you add another point on the other side
since I = ΣMR2 then this is 2MR2
What about a ring or circle, that is nothing more than a bunch of points all the same distance from the center
so how many points are there? The circumference
so I= πR2MR2
I know that different objects moment of inertia differ by a number in front, like 1/2 or 3/5
Why is their no number prefix for Inertia in front of the formula for a hoop/ hollow cylinder/ circle that represents its circumference? How is this even derived?
Second question, How do you represent the angular Kinetic energy of this object?
Right point = B
½ I ωA2 + ⅓ I ωB2
½ I ( ωA2+ωB2 )
both objects have same ω so
½ I 2ω2
Or
do I use ω to represent the angular velocity of the whole object and just keep it as
½ I ω2 with whatever I is from the previous question?