Why Can't Moment of Inertia Exceed MR² for Solid Bodies?

[andyrk]

How do we know that moment of inertia cannot exceed MR² for a solid body like solid cylinder, solid sphere, hollow sphere etc? R is the radius of the object in consideration.

I know it has something to do with- that for solid bodies (in some cases hollow also) there are a lot of point masses in the body which are not at a distance of R from the axis of rotation. They are closer (less than R) to the axis of rotation than the point masses on the boundary of the body (at a distance of R from the body). Still, how does it prove that in such cases the moment of inertia would be less than MR²?

∑m_ir_i =

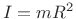or

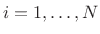So how do the above two equations show that if there are masses which are located at a distance of less than R from the axis of rotation then the moment of inertia would be less than MR²?

 

[ShayanJ]

The moment of inertial of a cylindrical shell around its axis is just M R^2. Now I can place anything I want at the centre of the shell(actually it can be anywhere!) and somehow connect it to the shell. Then the moment of inertial of the whole thing around the shell's axis is more that M R^2. So what you say is not true and so doesn't have a proof!

 

[robphy]

I think a part of your question deals with what M and R represent.
Is M the total mass of the object? Is R some maximum distance that a piece of the object is from the axis of rotation?

I teach moment of inertia by saying it has the form kMR^2, where M is the total mass and R is some characteristic length (like the radius).
The goal is to compute k.

If I have a cylindrical shell of mass M and radius R and a mass m is added at radius r (say aR where 0<=a<=1),
then the moment of inertia is
MR^2+m(aR)^2=(M+ma^2)R^2=\frac{M+ma^2}{M+m} (M+m)R^2=k M_{total}R^2.
Note: for nonzero m, the coefficient k equals 1 only when a=1, otherwise k<1.

 

[ShayanJ]

I think a part of your question deals with what M and R represent.
Is M the total mass of the object? Is R some maximum distance that a piece of the object is from the axis of rotation?

I teach moment of inertia by saying it has the form kMR^2, where M is the total mass and R is some characteristic length (like the radius).
The goal is to compute k.

If I have a cylindrical shell of mass M and radius R and a mass m is added at radius r (say aR where 0<=a<=1),
then the moment of inertia is
MR^2+m(aR)^2=(M+ma^2)R^2=\frac{M+ma^2}{M+m} (M+m)R^2=k M_{total}R^2.
Note: for nonzero m, the coefficient k equals 1 only when a=1, otherwise k<1.

So take a>1. Then k>1 !

EDIT:Sorry, I know this is wrong now!

 

[andyrk]

So take a>1. Then k>1 !

I am pretty sure on this part that moment of inertia can never cross MR². My main question was that why in most of the cases of solid bodies, it is always less than MR² and never equal to it?

Have a look at this link (its a PDF file): http://www.colorado.edu/physics/phys1110/phys1110_fa08/lectures/Lec31.pdf
Look at page 4 and 5. And look at the line which says
"Not all of the mass is at a distance R from the axis. So we end up with something less than MR²."

So my main question was that why do we end up with something less than MR²? I don't find "Not all of the mass is at a distance R from the axis" to be a sufficient enough reason for Moment of Inertia to be less than MR².

 

[ShayanJ]

Sorry for post #4. It was a misunderstanding!
I think we should think more carefully about the calculation presented by robphy!

 

[andyrk]

Sorry for post #4. It was a misunderstanding!
I think we should think more carefully about the calculation presented by robphy!

Yeah Shyan. Now when I look at the calculations of robphy closely I am able to understand how MOI would always be less than MR². Thanks for that robphy!

 

[andyrk]

But then what happens if we put a mass at a position which is greater than R? That is, what happens when a>1? Can this happen? Why or why not?

 

[ShayanJ]

But then what happens if we put a mass at a position which is greater than R? That is, what happens when a>1? Can this happen? Why or why not?

That's exactly my misunderstanding in post #4. If you have a mass with some length scale R and then add another mass somewhere farther, you're just extending the the object and so you'll just have a new length scale!

 

[andyrk]

That's exactly my misunderstanding in post #4. If you have a mass with some length scale R and then add another mass somewhere farther, you're just extending the the object and so you'll just have a new length scale!

So you mean wherever we place the new object that becomes the new R?

 

[ShayanJ]

So you mean wherever we place the new object that becomes the new R?

Yes, that's the point. Because actually by R, we mean a length scale which shows the extent of the object we're considering. I think its good to look at the moments of inertia of some shapes that don't involve circles!

 

[andyrk]

Yes, that's the point. Because actually by R, we mean a length scale which shows the extent of the object we're considering. I think its good to look at the moments of inertia of some shapes that don't involve circles!

Hmm...yeah I got that now. :)
And, I am talking about basic figures like cylinder, disc, ring, sphere etc. because that's what my curriculum asks for. But I think it would be the same explanation for other simple geometrical figures like square plate, cube, cuboid, rod etc. Won't it be?

 

[ShayanJ]

Hmm...yeah I got that now. :)
And, I am talking about basic figures like cylinder, disc, ring, sphere etc. because that's what my curriculum asks for. But I think it would be the same explanation for other simple geometrical figures like square plate, cube, cuboid, rod etc. Won't it be?

Take a look at here! You'll notice the difference.

 

[gracy]

I think a part of your question deals with what M and R represent.
Is M the total mass of the object? Is R some maximum distance that a piece of the object is from the axis of rotation?

I teach moment of inertia by saying it has the form kMR^2, where M is the total mass and R is some characteristic length (like the radius).
The goal is to compute k.

If I have a cylindrical shell of mass M and radius R and a mass m is added at radius r (say aR where 0<=a<=1),
then the moment of inertia is
MR^2+m(aR)^2=(M+ma^2)R^2=\frac{M+ma^2}{M+m} (M+m)R^2=k M_{total}R^2.
Note: for nonzero m, the coefficient k equals 1 only when a=1, otherwise k<1.

what is a?

 

[robphy]

a is a number between 0 and 1 describing the position r as a fraction of R, presumed to be the outer radius of the object.

 

[andyrk]

Take a look at here! You'll notice the difference.

The difference is that R changes to L in case of rods or l²+b² in case of squares, cubes and cuboids. The explanation that robphy gave still remains true even after different representations of R. Don't you agree?

 

[ShayanJ]

The difference is that R changes to L in case of rods or l²+b² in case of squares, cubes and cuboids. The explanation that robphy gave still remains true even after different representations of R. Don't you agree?

Yeah but about infinite disk and polygons things seem to be different. Maybe I'm confused again!

 

[sophiecentaur]

If you look at what you wrote in the initial post, you will see an Integral. That, in words, says that the Moment of Inertia is the sum (for all elemental parts of the object) of the mass of each particular element of mass times the distance from the CM squared. the maximum value that it can have (for a given diameter / width / length of object) is when all the elemental masses are distance R from the CM. If any masses are less than R from the CM, the MI will, of course be less than that Integral. That's just a bit of simple logic.

 

[andyrk]

If you look at what you wrote in the initial post, you will see an Integral. That, in words, says that the Moment of Inertia is the sum (for all elemental parts of the object) of the mass of each particular element of mass times the distance from the CM squared. the maximum value that it can have (for a given diameter / width / length of object) is when all the elemental masses are distance R from the CM. If any masses are less than R from the CM, the MI will, of course be less than that Integral. That's just a bit of simple logic.

I can't see how this is simple logic. Firstly, how can we add all the small moment of inertia to get the overall moment of inertia?

I (Moment of Inertia) = dm₁r₁²+dm₂r₂²...+ dm_nr_n² = kMR²​

Now if in some of the above terms , r_i is less than R and some it is equal than R then how can we know that the sum would be less than R?
Secondly, I don't understand how the above equation that I wrote can be ever mathematically proven to RHS. I mean if you take all the dm's common (I am assuming that all the differential point masses are of same mass) from the summation (in this case an integral) then you are just left with : dm(r₁² + r₂² + r₃²...r_n²)
It would eventually be something like- dm x (Some distance much greater than R² ), which is not even close to how the actual MOI is.

All the sum of squares in the parenthesis above would, by all means, be greater than R². Which is simply not possible! That's the reason I can't understand the way you put it in integral/summation. But what robphy wrote, it makes sense and also doesn't create any ambiguity.[/SUP]

 

[A.T.]

R is the radius of the object in consideration.

if in some of the above terms , r_i is less than R and some it is greater than R

How can any r_i be greater than the radius of the object? R = max(r_i) per definition.

 

[andyrk]

How can any r_i be greater than the radius of the object? R = max(r_i) per definition.

Sorry for the typo. I meant that in some it is equal to R not greater than R. I have corrected the error in the previous post.

 

[A.T.]

It would eventually be something like- dm x (Some distance much greater than R² ), which is not even close to how the actual MOI is.

How do you know that is not even close? The bracket is much more than R², but dm is much less than M.

 

[andyrk]

How do you know that is not even close? The bracket is much more than R², but dm is much less than M.

Hmm.. That's a good reason. But what I was saying was that the expression in the end doesn't look familiar to how moment of inertia in standard format looks. Something like- 1/2MR² etc. But this is weird because it is like a dm(r₁² + r₂² + r₃²...r_n²), which is not the same as the standard format.

 

[voko]

Assume you have a solid. Take an arbitrary point $C$ within the solid; then $R$ is the maximum distance of any point of the solid from $C$. Compute its moment of inertia with respect to $C$: $$ \int r^2 dm \le \int R^2 dm = R^2 \int dm = MR^2.$$

 

[andyrk]

Assume you have a solid. Take an arbitrary point $C$ within the solid; then $R$ is the maximum distance of any point of the solid from $C$. Compute its moment of inertia with respect to $C$: $$ \int r^2 dm \le \int R^2 dm = R^2 \int dm = MR^2.$$

What is r? And how does this post explain Post #23?

 

[voko]

$r$ is the distance from $C$, by definition of the moment of inertia.

 

[sophiecentaur]

How can any r_i be greater than the radius of the object? R = max(r_i) per definition.

Allowing for the fact that the Integral referred to is, actually, a Definite Integral (just not very accurately written) and that the symbol "R" was assumed to be the the upper limit of all the R1, R2, R3 etc, the maximum possible value will be when all the R's are equal to R.
If we had been strict in our mathematical notation then, perhaps, we wouldn't have had the misunderstanding. If you think about it, that integral can have no meaning / value unless R represents the maximum (say the radius of a disc / ring or the side of a square etc etc). Look up MI's of common shaped objects and the expression for MI doesn't involve an integral; that's be done already, over some dimension values.

 

[fireflies]

I think a part of your question deals with what M and R represent.
Is M the total mass of the object? Is R some maximum distance that a piece of the object is from the axis of rotation?

I teach moment of inertia by saying it has the form kMR^2, where M is the total mass and R is some characteristic length (like the radius).
The goal is to compute k.

If I have a cylindrical shell of mass M and radius R and a mass m is added at radius r (say aR where 0<=a<=1),
then the moment of inertia is
MR^2+m(aR)^2=(M+ma^2)R^2=\frac{M+ma^2}{M+m} (M+m)R^2=k M_{total}R^2.
Note: for nonzero m, the coefficient k equals 1 only when a=1, otherwise k<1.

Awesome derivation, I must say