- #1
Pascal1p
- 28
- 0
Homework Statement
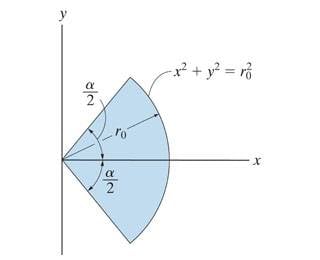
Determine the moment of inertia of the shaded area about the x-axis.
Homework Equations
I(x)= y^2dA
The Attempt at a Solution
In order to determine the moment of inertia of the shaded area about the x-axis I first looked at the portion above the x-axis, integrate it with a small rectangular element and then because of the symmetry I would multiply it with 2. So:
Yet if I integrate that with those limits and then multiply it with 2 and insert B= a/2
I do not get (a-sin (a))(r^4)/8. The answer I would get if I just use ∫∫((r*sinθ)^2)rdθdr. Which is the correct answer.
But why doesn't it work?