Understanding Moment of Inertia for a Beam Bending about the Y-Axis

[wahaj]

Homework Statement

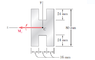
I'm supposed to solve for the maximum moment assuming the beam bends about the y-axis (not the z axis as shown in the image. Same image for different questions). I don't understand how to find the moment of inertia in this case. The solution gives the moment of inertia for the 80 x 16 mm part of the bar to be
$$I =\frac{1}{12}(80)(16^3) + 80(16)(16^3)$$
What I don't understand is where the 80(16)(16³) comes from. Can some one explain?

 

[SteamKing]

I don't understand either. Sometimes, the authors of these solutions use obscure methods to find the answers. If in doubt about the I calculation, use a method which you understand better.

You could calculate I for an 80x48 rectangle and then subtract out the I for each of the 24x16 insets:

Iy = (1/12)*80*48^3 - 2*(1/12)*24*16^3 mm^4

This is a simple method because the parallel axis theorem is not required (everything has the same centroidal location w.r.t. the y-axis.

 

[wahaj]

It's the stupid parallel axis theorem. I've only used that a few times before so I had completely forgotten about it. Your post reminded me of it. The second area moment of inertia using the parallel axis theorem is
$$I = I_x+Ar^2$$
here A is the area of the region. Anyways thanks for the help

 

[SteamKing]

It's the stupid parallel axis theorem. I've only used that a few times before so I had completely forgotten about it. Your post reminded me of it. The second area moment of inertia using the parallel axis theorem is
$$I = I_x+Ar^2$$
here A is the area of the region. Anyways thanks for the help

The only problem is, it doesn't match the calculation in the OP.

If you wanted to split the Iy calculation into three segments, then you would have the following:

center segment: A = 16 * 32 mm^2 Iy = (1/12)*32*16^3 mm^4; no PAT required

upper, lower segments: A = 16*80 mm^2 Iy = (1/12)*80*16^3 mm^4
PAT = 16*80*24^2 mm^4,

So, the total Iy =

(1/12)*32*16^3 + 2*[(1/12)*80*16^3 + 16*80*16^2] = 720,896 mm^4

Alternately, by subtracting the two 16 x 24 mm cutouts from the 80 x 48 mm rectangle:

Iy = (1/12)*80*48^3 - 2*[(1/12)*24*16^3] = 720,896 mm^4

 

[wahaj]

I realize I made a mistake in the OP. It's supposed to be 80(16)(16^2). However I like your second method better than the PAT.