Raghavendar Balaji
- 19
- 0
Homework Statement
1. Homework Statement
An uniform disk of mass m, thickness L and radius r is suspended from the ceiling by a wire. It is attached to the disk at a distance, d from the center of mass, so that it inclines at an angle A to the vertical. What is the moment of inertia of the inclined disk through that axis/string?
Homework Equations
I know that the MOI of a horizontal disc about the vertical perpendicular axis to the base is MR^2 /2.
The Attempt at a Solution
I did the problem initially without the parallel axis theorem, hinging the body to the center. I took an element dr at a distance of r × sin(A) to the vertical. Then dV = 2 × pi × r × dr × L and ρ = M/(pi × (R^2) × L). Then ∫(distance)^2 × ρ × dV. I got the answer which is ((M × R^2) × sin^2 (A)) /2, which is wrong, so I can't proceed to the next step.
Kindly help me regarding this.
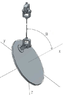
 . Considering that there are no product of inertia terms, the moment of inertia through the diameter i.e., Iyy and Izz are same, which is (MxR^2) / 4. So we know the matrix, now. And, initially when the vertical axis passes through the center, we won't need parallel axis theorem but if it is to be translated to a distance as shown in the diagram, I guess we need it. Am I fortunately right in this case?
. Considering that there are no product of inertia terms, the moment of inertia through the diameter i.e., Iyy and Izz are same, which is (MxR^2) / 4. So we know the matrix, now. And, initially when the vertical axis passes through the center, we won't need parallel axis theorem but if it is to be translated to a distance as shown in the diagram, I guess we need it. Am I fortunately right in this case?