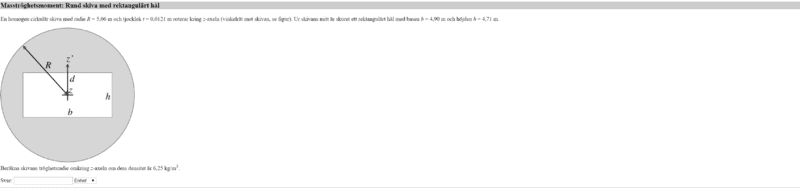
- #1
top12eaper
- 2
- 0
i know how to calculate the inersia for the cylinder, than i have to take away the inersia of the rectangel, but i can't find an equation for the inersia for a rectangel with the plane spinning perpendicular to the rotation axis, please help !