Moment of inertia of cylinder with a rectangel shaped hole

Click For Summary
SUMMARY

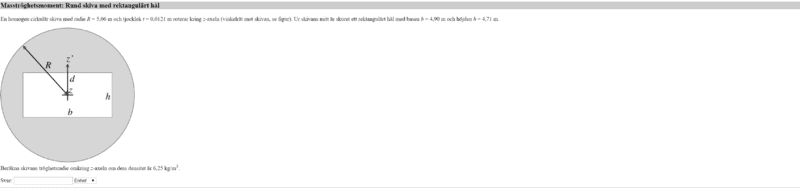
The discussion centers on calculating the moment of inertia for a cylinder with a rectangular hole. The user is familiar with the inertia of the cylinder but struggles to find the appropriate equation for the rectangular section when the plane spins perpendicular to the rotation axis. The conversation suggests deriving the formula using double integrals if the user is comfortable with that mathematical concept. Specific guidance on the axis of rotation is also sought to clarify the calculation process.

PREREQUISITES
  • Understanding of moment of inertia concepts
  • Familiarity with double integrals
  • Knowledge of rotational dynamics
  • Basic geometry of shapes, particularly cylinders and rectangles
NEXT STEPS
  • Research the derivation of moment of inertia for composite shapes
  • Study double integrals and their applications in physics
  • Explore the parallel axis theorem for moment of inertia calculations
  • Examine resources on rotational dynamics and inertia calculations
USEFUL FOR

Students and professionals in mechanical engineering, physics enthusiasts, and anyone involved in calculating moments of inertia for complex shapes.

top12eaper
Messages
2
Reaction score
0
i know how to calculate the inersia for the cylinder, than i have to take away the inersia of the rectangel, but i can't find an equation for the inersia for a rectangel with the plane spinning perpendicular to the rotation axis, please help !
fisyk.PNG
 
Physics news on Phys.org
Which axis do you want?
Does this wiki page help? Have you looked anywhere else for this info?
 
sophiecentaur said:
Which axis do you want?
Does this wiki page help? Have you looked anywhere else for this info?
dont think so, they give me the equation for the inersia about the x and y axis, in my case the axis pierces the plane of the rectangel.
 

Similar threads

Undergrad Moment of inertia of human body with limbs at an angle
  • · Replies 12 ·
Replies
12
Views
2K
Undergrad Resolve moment of inertia at an angle
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Moment of Inertia about an axis and Torque about a point
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Why Do Different Objects Share Similar Moments of Inertia?
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Inertia of body moving about two distinct parallel axes
  • · Replies 10 ·
Replies
10
Views
2K
High School Moment of Inertia of Rectangles
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad How find moment of inertia for car in turn?
  • · Replies 49 ·
2
Replies
49
Views
5K
Undergrad Axial angular momentum calculation
  • · Replies 30 ·
2
Replies
30
Views
4K
Graduate How can I calculate the moment of inertia of any object?
  • · Replies 10 ·
Replies
10
Views
2K
Undergrad Is it possible to create linear acceleration using nothing but different moments of inertia beteen a wheel and axle?
  • · Replies 5 ·
Replies
5
Views
2K