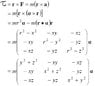SUMMARY
The discussion focuses on the derivation of the moment of inertia in vector form, specifically addressing the transition from the equation $$mr^2 \mathbf{α} = (r^2 I) \mathbf{α}$$ to the formation of a 3x3 matrix. Participants clarify the components of the vector representation and how to express the matrix in terms of the angular acceleration vector $$\mathbf{α}$$. The final matrix representation is confirmed as $$\left(\begin{array}{ccc} x^2 & xy & xz \\ xy & y^2 & yz \\ xz & yz & z^2 \end{array}\right)\mathbf{α}$$, illustrating the relationship between the moment of inertia and the angular acceleration.
PREREQUISITES
- Understanding of vector calculus and matrix operations
- Familiarity with the concepts of torque and moment of inertia
- Knowledge of angular acceleration and its representation in vector form
- Basic proficiency in linear algebra, particularly in constructing and manipulating matrices
NEXT STEPS
- Study the derivation of the moment of inertia tensor in three-dimensional space
- Learn about the physical significance of the inertia matrix in rotational dynamics
- Explore applications of angular acceleration in rigid body motion
- Review linear algebra concepts related to eigenvalues and eigenvectors of matrices
USEFUL FOR
Students and professionals in physics, mechanical engineering, and applied mathematics who are working on problems involving rotational dynamics and the mathematical representation of physical systems.