- #1
asi123
- 258
- 0
Homework Statement
Hey guys.
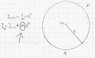
So I got this circle (full circle), and I need to find the moment of inertia in point A.
So, of curse I use the parallel axis theorem.
The thing that got me confuse is what's m (in the pic), I mean, it should be the mass at point A, right?
so why, in the examples I saw, they choose it to be the mass of entire circle?
10x.