Kingyou123
- 98
- 0
Homework Statement
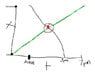
Check attached image. Is there any point along the path that he passes at the same time each day
Homework Equations
None that I know of...
The Attempt at a Solution
The whiteboard image, I'm not sure if that's how the graph is suppose to look like.