Frozen Light
- 14
- 0
Homework Statement
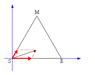
At a certain instant, the earth, the moon, and a stationary 1030kg spacecraft lie at the vertices of an equilateral triangle whose sides are 3.84×10^5km in length.
Find the magnitude of the net gravitational force exerted on the spacecraft by the Earth and moon.
Homework Equations
GMm/r^2 = Fg
r = 3.84*10^5 km
Me = 5.98*10^24 kg
Mm = 7.35*10^22 kg
G = 6.67*10^-11
Ms = 1030kg
The Attempt at a Solution
http://imgur.com/p8OBdfd
I think it's probably a simple error somewhere but I've gotten about 3-4 different answers all which are not F=2.8N - I've tried calculating it at different stages in the algebra - are the angles somehow not based off 60*? I don't know what it's missing.
Last edited: