Motion along a straight line by a car

Click For Summary
SUMMARY

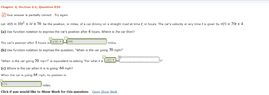
The discussion focuses on expressing the velocity of a car using function notation in the context of motion along a straight line. The user seeks clarification on how to represent the question "When is the car going 70 mph" using the notation v(t). It is established that v(t) typically denotes velocity at time t, while s(t) represents the position function. The correct formulation to find when the car reaches 70 mph is to set the derivative of the position function, s'(t), equal to 70, resulting in the equation s'(t) = 70.

PREREQUISITES
  • Understanding of function notation in mathematics
  • Knowledge of derivatives and their application in motion
  • Familiarity with velocity and speed concepts
  • Basic calculus principles
NEXT STEPS
  • Study the concept of derivatives in calculus
  • Learn how to apply function notation in real-world scenarios
  • Explore the relationship between position, velocity, and acceleration
  • Investigate practical examples of motion along a straight line
USEFUL FOR

Students studying calculus, educators teaching motion concepts, and anyone interested in applying mathematical principles to real-world motion scenarios.

Nero1
Messages
1
Reaction score
0
Part B of the following problem seems to be fairly straightforward, but I can't seem to understand it properly. I might be overthinking the problem entirely.

Would anyone be willing to help?
 

Attachments

  • Screenshot (3).png
    Screenshot (3).png
    17.4 KB · Views: 112
Mathematics news on Phys.org
(b) asks you to "use function notation" to express the question "When is the car going 70 mph". On the left side of the equal sign you have "v(t)". Were you given that or did you choose it? Often "v(t)" is used to indicate the speed or velocity at time t but there is nothing in the problem that defines v(t). The only thing defined here is s(t). The speed, at time t, is the derivative of that, s'(t). I would answer s'(t)= 70.
 

Similar threads

High School Cartesian Space vs. Euclidean Space
  • · Replies 10 ·
Replies
10
Views
2K
MHB Homework: Bisectors and Intersection Points of Straight Lines
  • · Replies 1 ·
Replies
1
Views
3K
Moving in a straight line with multiple constraints
  • · Replies 98 ·
4
Replies
98
Views
6K
MHB What is the maximum distance of P from point O during the motion?
  • · Replies 10 ·
Replies
10
Views
2K
MHB Mechanics- general motion in a straight line.
  • · Replies 2 ·
Replies
2
Views
2K
Studying Poor at problem solving -- I'm looking for changes to my approach
  • · Replies 6 ·
Replies
6
Views
943
Time dilatation between straight and curved lines in Minkowsi space
  • · Replies 19 ·
Replies
19
Views
2K
Undergrad Line count in a simple program
  • · Replies 16 ·
Replies
16
Views
3K
Undergrad Non-uniform Circular Motion & Acceleration
  • · Replies 8 ·
Replies
8
Views
2K
Graduate Car in corner -- relative airflow
  • · Replies 20 ·
Replies
20
Views
4K