Movement with sine acceleration

[yaqwsx]

Hello,
first of all, excuse my English. I have no experience witch describing mathematics problems in English.
I have a movement with sine acceleration. I need to get equation of velocity depending on track (I am not sure if that's the right expression in English - on the traveled distance).
Here's my equation for acceleration: a = A * sin(∏*t/T)

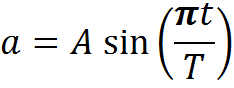
where a is acceleration, A is the maximal acceleration, t is actual time and T is the whole time of accelerating. I want to get a velocity, so I integrated this expression and added parameter c to satisfy the condition: when t = 0, v = 0. I got this equation: v = (A*T/∏)*(1-cos(pi*t/T))

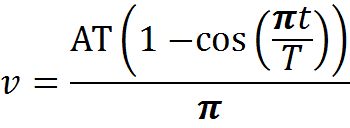
If I wanted dependency veleocity on time, this would be enought, but I wanted depency velocity on track, so I have integrated... s = A*T*(∏*t - T*sin(∏*t/T))/∏^2

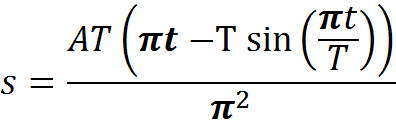
I wanted to express t from this equation and put it into expression for velocity. For that I need to solve an equation in form a*x +sin(b*x) = c, which I can't solve. And as I have read it isn't something easy...
How can I get dependency of velocity on track for this movenent? I think there has to be a simple solution, but I don't see it. Can you help me, please?

 

[gsal]

can you just simply isolate AT from the equation for s and replace AT with it in the equation for v?

 

[yaqwsx]

I think isolating AT won't help me - T is the whole time of accelerating - it's a constant. A is also a constnt. I need get rid of t - which is a variable and create dependency with s.