Sine/Cosine behaving like a linear function

[Neck]

Hello all. After completing a problem in which we derived the formulas for potential and spring force energy as functions of time, with simple harmonic motion I noticed the equations are EXACTLY the same, but with sine and cosine switched. The equations were:

A sin^2(pi * t)
A cos^2(pi * t)

I apologize for this awful format, I want to learn the math script used on this website, but I forgot the name (would be appreciated also).

Anyways here is a graph of the aforementioned functions.

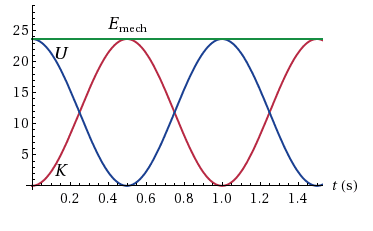
My question: Is there a way to represent this back and forth behavior with a linear function or any other way?

 

[jedishrfu]

If you use the series representation of a sin or cos function then you can see that it can never be represented by a linear function.

https://en.m.wikipedia.org/wiki/Sine#Series_definition

 

[mfb]

Both functions are not linear.

If two functions f,g are shifted by a fixed amount with respect to each other, then f(x)=g(x+c) for some constant c. Here $\cos(x)=\sin(x+\frac \pi 2)$, for example. Sine and cosine are also periodic, so you have additional relations like $\sin(x)=\sin(x+2n \pi) = \cos(x+2n \pi - \frac \pi 2)$ for every integer n.

 

[gmax137]

the math script used on this website

LaTeX.

 

[lekh2003]

I apologize for this awful format, I want to learn the math script used on this website, but I forgot the name (would be appreciated also).

https://www.physicsforums.com/help/latexhelp/
This link will help you learn LaTeX for PF

 

[Mark44]

If you use the series representation of a sin or cos function then you can see that it can never be represented by a linear function.

But you can approximate either of these functions in small intervals by straight lines.

Near x = 0, $\sin(x) \approx x$ and $\cos(x) \approx 1$. Notice that these are the first terms of the Maclaurin series for each of these functions.

 

[FactChecker]

My question: Is there a way to represent this back and forth behavior with a linear function or any other way?

The "back and forth" behavior is a trade-off between the two things. Combining those two into one equation is motivation for Euler's formula involving complex variables: e^iθ = cos(θ) + i ⋅ sin(θ). (There is a reason for using θ as though these are functions of angle rather than functions of t=time.) That one equation can be used to represent how the two things trade-off.
(see https://en.wikipedia.org/wiki/Euler's_formula )

PS. I see that the wikipedia article goes into a lot of advanced subjects that are not appropriate for this thread. The first paragraph is appropriate. This may be better: https://betterexplained.com/articles/intuitive-understanding-of-eulers-formula/

 

[Charles Link]

The reason for your graph being what it is in the OP is that $v=v_o \sin(\omega t)$, so that the kinetic energy $K.E.=(\frac{1}{2})mv^2=(\frac{1}{2})mv_o^2 \sin^2(\omega t)$. In order for the total energy $E$ to be constant, we must have the potential energy $U=(\frac{1}{2})m v_o^2 \cos^2(\omega t)$, because $\cos^2 (\theta)+\sin^2(\theta)=1$. $\\$ It may also interest you that $\cos^2(\omega t)=(\frac{1}{2})(\cos(2 \omega t)+1)$ , and $\sin^2(\omega t)=(\frac{1}{2})(1-\cos(2 \omega t))$. This is why the two curves in the graph of the OP are essentially sinusoidal.

 

[Neck]

LaTeX.

thank you! will learn that asap