somasimple
Gold Member
- 765
- 5
Hi all,
Here is my problem:
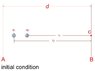
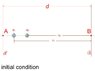
Two positive points charges are situated as the initial figure:
1/ How to compute the voltage between A and B (or C)?
2/ If the final condition is like described in the second figure, what is now the voltage between A and B.
3/ if the transition between the two states takes a time t1, does the speed of this transition changes something about the voltage that exists between A and B?
Thanks.
Here is my problem:
Two positive points charges are situated as the initial figure:
1/ How to compute the voltage between A and B (or C)?
2/ If the final condition is like described in the second figure, what is now the voltage between A and B.
3/ if the transition between the two states takes a time t1, does the speed of this transition changes something about the voltage that exists between A and B?
Thanks.