phunphysics2
- 29
- 0
U=kqoq/r ?
Please look at the attachments. I was wondering if someone could please check my work. That is all.
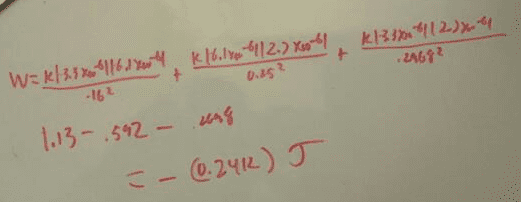

Thank you for your time!
Please look at the attachments. I was wondering if someone could please check my work. That is all.
Thank you for your time!