- #1
ashah99
- 60
- 2
- Homework Statement
- Please see attached problem
- Relevant Equations
- MSE = E( (Xhat[k] - X[k])^2 )
Hello all, I would appreciate any guidance to the following problem. I have started on parts (a) and (b), but need some help solving for the coefficients. Would I simply take the expressions involving the coefficients, take the derivative and set it equal to 0 and solve? I believe I also need the variance (for part (c) for instance) ##Var(U_K)## but using the formula (b-a)^2/12 (which would be (3-(-3)^2/12 = 3) from the uniform distribution seems wrong. Any help appreciated
Problem:

Approach so far:
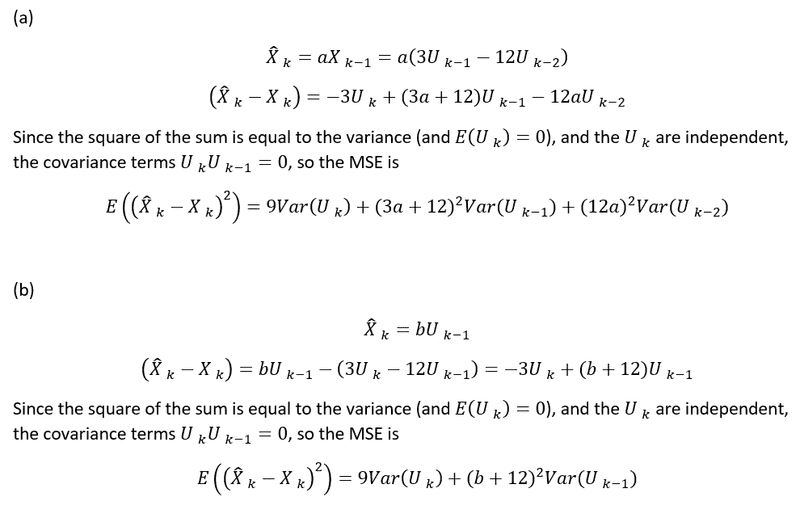
Problem:
Approach so far: