Multiple dielectrics inserted in capacitor

[member 392791]

Homework Statement

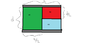
A parallel-plate capacitor is constructed by filling
the space between two square plates with blocks of three
dielectric materials, as in Figure P26.61. You may assume
that l >> d. (a) Find an expression for the capacitance of
the device in terms of the plate area A and d, κ1, κ2, and
κ3. (b) Calculate the capacitance using the values
A = 1.00 cm2, d = 2.00 mm, κ1 = 4.90, κ2 = 5.60, and
κ3 = 2.10.

Homework Equations

The Attempt at a Solution

I understand that κ1 is parallel to κ2 and κ3 and just make a circuit out of it. The problem I'm having is that it is saying the expression for the capacitance of κ1 is

κ1ε(A/2)/d

and for the capacitors of κ2 and κ3

κ2ε(A/2)/(d/2) and κ3(A/2)/(d/2)

However, my question is why for K2 and K3 isn't it Kε(A/4)/(d/2) since they only consist of one fourth the area of the whole capacitor

 

[NascentOxygen]

However, my question is why for K2 and K3 isn't it Kε(A/4)/(d/2) since they only consist of one fourth the area of the whole capacitor

K1 has half of the area of each square plate. The combination K2 with K3 can be viewed as a pair of capacitors in series.