- #1
Karl Karlsson
- 104
- 12
- Homework Statement
- A liquid flows in a cylindrical tube with the z-axis as the axis of symmetry and radius R. The flow rate of the liquid is given by $$ \vec v = \frac {p_0} {4lμ} (R^2-ρ^2)$$
where ##\frac {p_0} {l}## is the pressure drop in the pipe per unit length, ##μ## is the viscosity of the liquid and ##ρ## is the radial cylinder coordinate. Calculate ##∇\cdot\vec v## and ##∇^2\cdot\vec v##
- Relevant Equations
- $$ \vec v = \frac {p_0} {4lμ} (R^2-ρ^2)$$
Here is how my teacher solved this:
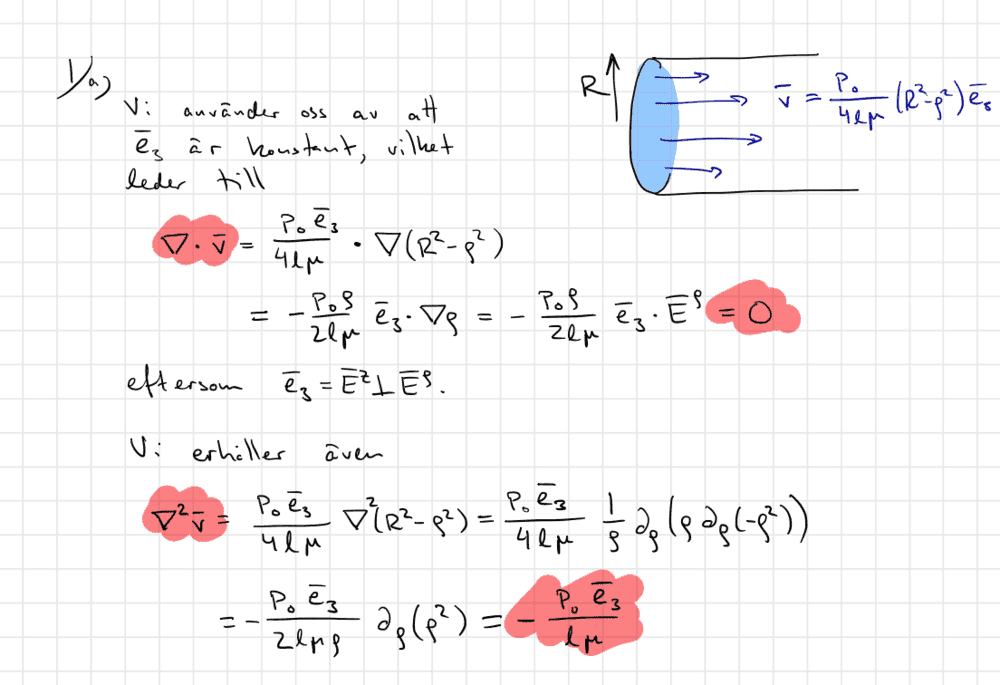
I understand what the nabla operator does, ##∇\cdot\vec v## means that I am supposed to calculate ##\sum_{n=1}^3\frac {d\vec v} {dx_n}## where ##x_n## are cylindrical coordinates and ##\vec e_3 = \vec e_z##. I understand why ##∇\cdot\vec v = 0##, I would get the same answer as my teacher if I used ##\sum_{n=1}^3\frac {d\vec v} {dx_n}## to calculate it. However when I calculate ##∇^2\cdot\vec v## I don't get the same answer. I would get ##∇^2\cdot\vec v = (∇\cdot (∇v_1),∇\cdot (∇v_2),∇\cdot (∇v_3)) = \frac {p_0} {4lμ}\cdot (0,0, ∇\cdot (∇(R^2-ρ^2))) =\frac {p_0} {4lμ}\cdot (0,0, \frac {\partial^2 (R^2-ρ^2)} {\partial ρ^2})##. Which is not equal to what my teacher got. Did I miss something? Also could someone explain the steps he took to arrive at his answer?
Thanks in advance!
I understand what the nabla operator does, ##∇\cdot\vec v## means that I am supposed to calculate ##\sum_{n=1}^3\frac {d\vec v} {dx_n}## where ##x_n## are cylindrical coordinates and ##\vec e_3 = \vec e_z##. I understand why ##∇\cdot\vec v = 0##, I would get the same answer as my teacher if I used ##\sum_{n=1}^3\frac {d\vec v} {dx_n}## to calculate it. However when I calculate ##∇^2\cdot\vec v## I don't get the same answer. I would get ##∇^2\cdot\vec v = (∇\cdot (∇v_1),∇\cdot (∇v_2),∇\cdot (∇v_3)) = \frac {p_0} {4lμ}\cdot (0,0, ∇\cdot (∇(R^2-ρ^2))) =\frac {p_0} {4lμ}\cdot (0,0, \frac {\partial^2 (R^2-ρ^2)} {\partial ρ^2})##. Which is not equal to what my teacher got. Did I miss something? Also could someone explain the steps he took to arrive at his answer?
Thanks in advance!