Malby
- 15
- 0
A mass m is confined to move in a channel in the x-direction and is connected to four identical springs with spring constant k, which are oriented at angles \phi = 45° as shown, if the system is in static equilibrium.
a) Ignoring friction, determine the natural frequency of vibration of the system.
b) What is the natural frequency, if the springs are oriented at equal but arbitrary angles \phi?
\omegan = \sqrt{\frac{k}{m}}
Not quite sure how to go about this one. I figure you need to take a small displacement of the system to the right or less then analyse the forces such that \SigmaF = ma, and then derive the standard form of the spring equation from there.
Any hints would be helpful!
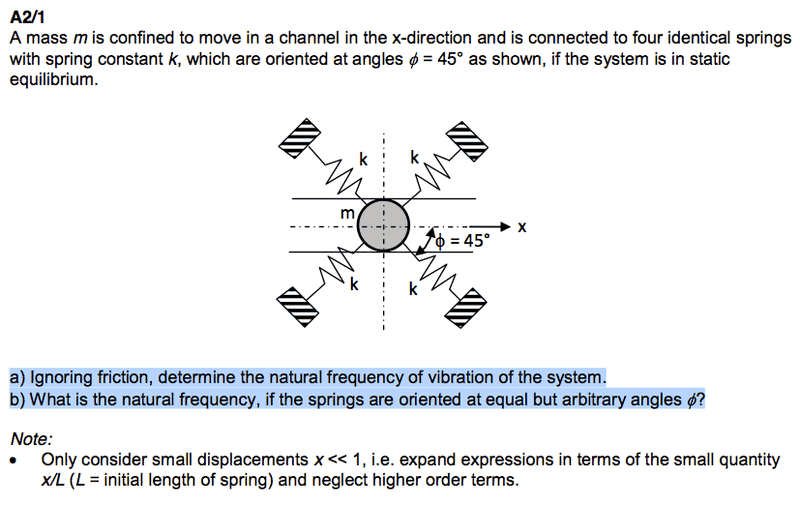
a) Ignoring friction, determine the natural frequency of vibration of the system.
b) What is the natural frequency, if the springs are oriented at equal but arbitrary angles \phi?
\omegan = \sqrt{\frac{k}{m}}
Not quite sure how to go about this one. I figure you need to take a small displacement of the system to the right or less then analyse the forces such that \SigmaF = ma, and then derive the standard form of the spring equation from there.
Any hints would be helpful!