- #1
Natural Log Limits: Understanding the Use of L'Hôpital's Rule
Click For Summary
Homework Help Overview
The discussion revolves around the application of L'Hôpital's Rule in the context of limits involving natural logarithms. Participants express confusion regarding the manipulation of logarithmic expressions and the steps leading to specific limit evaluations.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
- Participants inquire about the reasoning behind the introduction of natural logarithms in limit problems and the specific algebraic manipulations used. Questions arise about the choice of variables and the transformations applied to expressions.
Discussion Status
Several participants are actively seeking clarification on specific steps and the rationale behind them. There is an ongoing exploration of different interpretations of the problem, particularly regarding the use of logarithmic properties and the application of L'Hôpital's Rule.
Contextual Notes
Some participants note the presence of indeterminate forms in the limits being discussed, which justifies the use of L'Hôpital's Rule. There is also mention of the need for careful algebraic manipulation to facilitate limit evaluation.
- #2
lanedance
Homework Helper
- 3,304
- 2
pics always take a while to clear, you;re better writing it up if you can
- #3
bobber205
- 26
- 0
Didn't realize that. Sorry. :)
- #4
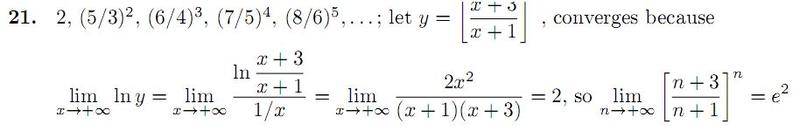
slider142
- 1,016
- 72
bobber205 said:Didn't realize that. Sorry. :)
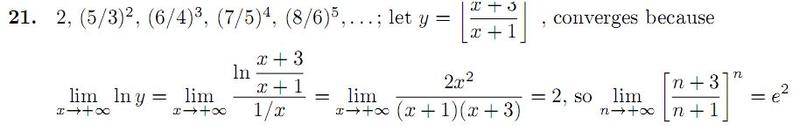
which equality in particular are you having a problem with? Or is it the introduction of the natural logarithm on the left-hand side?
- #5
bobber205
- 26
- 0
I am having trouble with why he choose to let y what it does and how we went on from there.
How did he get
ln ((x+3)(x+1)/(1/x))
How did he get
ln ((x+3)(x+1)/(1/x))
- #6
slider142
- 1,016
- 72
bobber205 said:
This makes each term in the sequence y(x). It is also trivial that y(x) = eln(y(x)), which, in this case, is easier to study. He made use of the logarithm rule: ln(ax) = xln(a), and algebra: x = 1/(1/x), provided x is not 0.
Many limits are easily solved if you can find a clever rewriting of the algebraic expression like this.
- #7
bobber205
- 26
- 0
How did he arrive at the 2x^2 / (x+3)(x+1) step? Is there something I'm missing he did when he took the limit to infinity?
- #8
slider142
- 1,016
- 72
bobber205 said:
The second limit gives us the indeterminate form 0/0, which makes it valid to use L'Hôpital's rule. This was the point of writing x as 1/(1/x).
Similar threads
- · Replies 5 ·
- · Replies 3 ·
- · Replies 9 ·
- · Replies 7 ·
- · Replies 2 ·
- · Replies 6 ·
- · Replies 3 ·