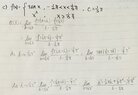SUMMARY
The discussion centers on determining the differentiability of the piecewise function defined as \( f(x) = \begin{cases} \tan x & \text{if } -\frac{\pi}{2} \le x < \frac{\pi}{3} \\ x^2 & \text{if } x \ge \frac{\pi}{3} \end{cases} \). It is concluded that the function is not differentiable at \( x = c \) due to discontinuity and the non-existence of certain limits. Specifically, the one-sided limits at \( x = c \) do not converge, confirming the lack of differentiability. The intermediate value property of derivatives is also highlighted as a relevant concept.
PREREQUISITES
- Understanding of piecewise functions
- Knowledge of limits and continuity
- Familiarity with trigonometric functions, particularly tangent
- Basic concepts of derivatives and differentiability
NEXT STEPS
- Study the properties of piecewise functions in calculus
- Learn about the intermediate value theorem in the context of derivatives
- Explore the concept of limits and their applications in differentiability
- Investigate the behavior of trigonometric functions near their discontinuities
USEFUL FOR
Students and educators in calculus, mathematicians analyzing differentiability, and anyone studying the behavior of piecewise functions and their derivatives.