How Do You Calculate Deflection in a Simply Supported Overhanging Beam?

[Rhysmachine]

Hey all, first post!

Looking to find a deflection equation for a simply supported overhanging beam with two supports and a point- load at the end of the canteliever. I can determine reactions at the supports but i am having trouble finding deflection between the supports.

Any help is appreciated!

the beam in question looks like (a) in the following picture but if we call L/2 a, instead.

 

[SteamKing]

This is a tricky problem. A simply supported beam with an overhanging load and no other appreciable loading is statically unstable. You have not provided any details about your calculations, so I am unable to comment on their validity. The so-called 'conjugate beam' you show reflects different end conditions from the original beam. The slope and deflection at C for the 'conjugate beam' must both vanish, whereas neither vanish at C for the given beam.

 

[Rhysmachine]

Sorry my mistake; the beam is restrained at A, vertically so I guess the triangle needs to be pointing the other way. The beam is no longer statically unstable now, right?

Ive done a number of calcs intergrating something like: P*a*x/LEI, with a number of variations to find slope then deflection, But I always seem to be ending up with an answer that would be mm^2 instead of mm. I was hoping someone might be able to go through finding the answer for me so I can find the deflection at many points along the A-B section.

Oh and the second example shouldn't be there at all. I just had to find a picture that was something like the problem I have as I couldn't upload my own pic.

 

[jhae2.718]

I'd solve the beam equation to find the displacement as a function of x or get an approximate solution using virtual work or finite elements.

 

[alphy]

Hi there,

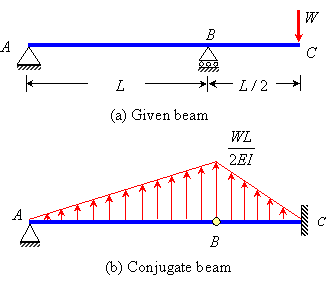
Deflection equations for overhanging beams can be quite complex, but I can offer some guidance to help you find the deflection between the supports. The deflection equation for a simply supported beam with a point load at the end of the cantilever is:

𝛿 = (PL^3)/(3EI)

Where P is the point load, L is the length of the beam, E is the Young's modulus, and I is the moment of inertia of the cross-section of the beam.

For an overhanging beam with two supports, the deflection equation becomes:

𝛿 = (PL^3)/(48EI)

Where P is still the point load, but L is now the distance between the two supports.

In your case, since the beam is overhanging, the distance between the supports is L/2. So, the deflection equation for your beam would be:

𝛿 = (PL^3)/(48EI)

I hope this helps. If you need any further clarification, please let me know. Good luck with your project!