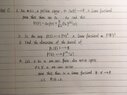BaconInDistress
- 2
- 0
I not very good at using the LaTex editor, so I took a photo of my HW questions.
View attachment 8831
For the first question, I'm not really sure how to get started, should I write out a specific case? Like what would $$\varphi (P)$$ be when m=1?
For the second question, I know that a linear functional have two properties, one being $$\varphi(u +v) = \varphi(u) + \varphi(v)$$ and the other one being $$\varphi(\lambda u) = \lambda\varphi(u)$$. I'm a bit confused about the mapping, is it saying that when we have a polynomial P(z), the map makes it goes to p(0) for all z?
View attachment 8831
For the first question, I'm not really sure how to get started, should I write out a specific case? Like what would $$\varphi (P)$$ be when m=1?
For the second question, I know that a linear functional have two properties, one being $$\varphi(u +v) = \varphi(u) + \varphi(v)$$ and the other one being $$\varphi(\lambda u) = \lambda\varphi(u)$$. I'm a bit confused about the mapping, is it saying that when we have a polynomial P(z), the map makes it goes to p(0) for all z?
Attachments
Last edited by a moderator: