- #1
kostoglotov
- 231
- 6
Currently working through a chapter on op amp circuits, fundamentals.
Came upon this practice problem in the section on inverting op amps
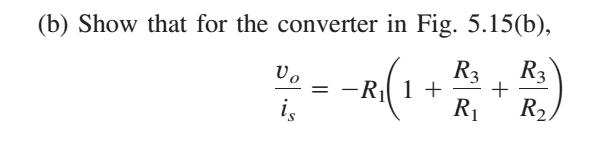
imgur link: http://i.imgur.com/2DrQLXk.png
imgur link: http://i.imgur.com/7KRKzKC.png
A working of this problem is not given. I got the correct answer the second time, by working through some KCL equations on a more fundamental level, but failed the first attempt based on what is evidently an incorrect assumption. But I don't fully understand why that assumption is wrong.
Before both solutions, I converted the current source to a voltage source in series with a resistor R_s with the equation V_s = i_s R_s.
I've labeled the node between R_1, R_2, and R_3 as v_2. v_1 is between R_s and the inverting input to the op amp.
My second attempt combined
\frac{-v_s}{R_1} = \frac{v_2-v_0}{R_3} + \frac{v_2}{R_2} \\ \text{with} \ \ v_2 = -i_1 R_1 \\ \text{and} \ \ i_1 = i_s
to obtain the correct proof.
My first wrong attempt made an assumption about calculating the equivalent resistance of R_1, R_2, and R_3, that goes like this:
-- you can think of R_1, R_2, and R_3 as being a "single resistance" as their combined configuration ("lump") takes v_0 to Ground (a zero Volt node). Because the node v_1 is (theoretically/ideally) at zero volts because it is short circuited to the common analog ground because we are considering an ideal op amp, and for an ideal op amp we can think of the op amps input terminals as being a short circuit when doing voltage calculations (and as an open circuit when doing current calculations). The presence of the R_s resistor connected to v_1 can be ignored, because it will not (ideally) change the fact that v_1 is (ideally) always 0V.
So, using this assumption, R_3 goes from v_0 into a two parallel resistors R_1, and R_2 which both (ideally) connect to the common analog ground node...soo
R_{eq} = R_3 + \frac{R_1 R_2}{R_1 + R_2}
and
v_0 = \frac{-R_{eq}}{R_s} v_s = -R_{eq} i_s
This of course does not work. In that it does not agree with the text or the also much more sound reasoning from just doing the KCL equations outlined initially.
What I don't understand really, is what's wrong with my reasoning in the assumption I constructed above, keeping in mind that this assumption would only work for ideal op amps (ie, v_1 is assumed as always being at 0V).
Came upon this practice problem in the section on inverting op amps
imgur link: http://i.imgur.com/2DrQLXk.png
imgur link: http://i.imgur.com/7KRKzKC.png
A working of this problem is not given. I got the correct answer the second time, by working through some KCL equations on a more fundamental level, but failed the first attempt based on what is evidently an incorrect assumption. But I don't fully understand why that assumption is wrong.
Before both solutions, I converted the current source to a voltage source in series with a resistor R_s with the equation V_s = i_s R_s.
I've labeled the node between R_1, R_2, and R_3 as v_2. v_1 is between R_s and the inverting input to the op amp.
My second attempt combined
\frac{-v_s}{R_1} = \frac{v_2-v_0}{R_3} + \frac{v_2}{R_2} \\ \text{with} \ \ v_2 = -i_1 R_1 \\ \text{and} \ \ i_1 = i_s
to obtain the correct proof.
My first wrong attempt made an assumption about calculating the equivalent resistance of R_1, R_2, and R_3, that goes like this:
-- you can think of R_1, R_2, and R_3 as being a "single resistance" as their combined configuration ("lump") takes v_0 to Ground (a zero Volt node). Because the node v_1 is (theoretically/ideally) at zero volts because it is short circuited to the common analog ground because we are considering an ideal op amp, and for an ideal op amp we can think of the op amps input terminals as being a short circuit when doing voltage calculations (and as an open circuit when doing current calculations). The presence of the R_s resistor connected to v_1 can be ignored, because it will not (ideally) change the fact that v_1 is (ideally) always 0V.
So, using this assumption, R_3 goes from v_0 into a two parallel resistors R_1, and R_2 which both (ideally) connect to the common analog ground node...soo
R_{eq} = R_3 + \frac{R_1 R_2}{R_1 + R_2}
and
v_0 = \frac{-R_{eq}}{R_s} v_s = -R_{eq} i_s
This of course does not work. In that it does not agree with the text or the also much more sound reasoning from just doing the KCL equations outlined initially.
What I don't understand really, is what's wrong with my reasoning in the assumption I constructed above, keeping in mind that this assumption would only work for ideal op amps (ie, v_1 is assumed as always being at 0V).