Nellie Newton hangs at rest from the ends of the rope as shown.

[pbody]

1. Nellie Newton hangs at rest from the ends of the rope as shown. How does the reading on the scale compare with her weight?

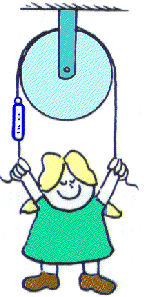2. ANSWER FROM BOOK.

The scale will read half her weight. In this way, the net force (upward pull of left rope + upward pull of right rope rope weight = 0

3. Can somebody explain to me what the answer means, and how I can understand this better?

How would I know it would read half her weight?

 

[CWatters]

She isn't moving so the total of all forces acting on her must sum to zero. If we take UP as positive then that sum looks like this...

upward pull of left rope + upward pull of right rope - weight = 0

or by rearranging that..

upward pull of left rope + upward pull of right rope = weight... Equation 1

Since she is symetrical we can also write...

upward pull of left rope = upward pull of right rope......Equation 2

Substitute into Equation 1 gives

upward pull of left rope + upward pull of left rope = weight

rearrange..

2 * upward pull of left rope = weight

rearrange..

upward pull of left rope = weight/2

similarly for the right rope.

 

[pbody]

She isn't moving so the total of all forces acting on her must sum to zero. If we take UP as positive then that sum looks like this...

upward pull of left rope + upward pull of right rope - weight = 0

or by rearranging that..

upward pull of left rope + upward pull of right rope = weight... Equation 1

Since she is symetrical we can also write...

upward pull of left rope = upward pull of right rope......Equation 2

Substitute into Equation 1 gives

upward pull of left rope + upward pull of left rope = weight

rearrange..

2 * upward pull of left rope = weight

rearrange..

upward pull of left rope = weight/2

similarly for the right rope.

How exactly should I know this, I will check again but I don't think the book describes this at all. I would just like to know so I can get a little more practice and know what I am doing, instead of relying on the back of the book to confuse me.

** By any chance does it have to deal with Support Force?

Thank you

 

[pbody]

How exactly should I know this, I will check again but I don't think the book describes this at all. I would just like to know so I can get a little more practice and know what I am doing, instead of relying on the back of the book to confuse me.

** By any chance does it have to deal with Support Force?

Thank you

Because if it is on Support Force this is the exert I was given by the book to help me answer this question.

Consider a book lying at rest on a table. It is in equilibrium. What forces act on the book? One force is that due to gravity - the weight of the book. Since the book is in equilibrium, there must be another force acting on the book to produce a net force of zero --an upward force opposite to the force of gravity. The table exerts this upward force. We call this the upward support force. This upward support force, often called the normal force, must equal the weight of the book. If we call the upward force positive then the downward weight is negative and the two add to become zero. The net force on the book is zero. Another way to say the same thing is ƩF = 0

To understand better that the table pushes up on the book, compare the case of compressing a spring. If you push the spring down, you can feel the spring pushing up on your hand. Similarly, the book lying on the table compresses atoms in the table, which behave like microscopic springs. The weight of the book squeezes downward on the atoms and they squeeze upward on the book. In this way, the compressed atoms produce the support force.

When you step on a bathroom scale, two forces act on the scale. One is your downward push on the scale -- result of gravity pulling on you -- and the other is the upward support force of the floor. These forces squeeze a mechanism (in effect, a spring) within the scale that is calibrated to show the magnitude of the support force. It is this support force that shows your weight. When you weigh yourself on a bathroom scale at rest, the support force and the force of gravity pulling you down have the same magnitude. Hence we can say that your weight is the force of gravity acting on you.

 

[CWatters]

She isn't moving so the total of all forces acting on her must sum to zero.

Comes from Newtons First Law..

http://en.wikipedia.org/wiki/Newton's_laws_of_motion

First law: If an object experiences no net force, then its velocity is constant: the object is either at rest (if its velocity is zero), or it moves in a straight line with constant speed (if its velocity is nonzero).

The rest is reasonably straightforwards maths.

By any chance does it have to deal with Support Force

My answer looked at the forces acting on her because it referred to the "upward pull" of the left/right rope. You could also solve it by looking at the forces on the pulley because that isn't moving either..

upward pull of support - downward pull of left rope - downward pull of right rope = zero

Obviously the support must carry her weight so "upward pull of support" = weight.

Rearrange and you get same result.

 

[CWatters]

Because if it is on Support Force this is the exert I was given by the book to help me answer this question.

Consider a book lying at rest on a table. It is in equilibrium. What forces act on the book? One force is that due to gravity - the weight of the book. Since the book is in equilibrium, there must be another force acting on the book to produce a net force of zero...

Yes that's the key to solving the problem.

--an upward force opposite to the force of gravity. The table exerts this upward force. We call this the upward support force.

In the case of the book there is a reaction force which they call a support force, however the term "support force" isn't generally used in physics. Better call it the reaction force. It results from the book trying to compress the table.

In the case of the girl on the ropes you have gravity acting downwards. That stretches the ropes which (when they have stopped stretching) causes them to create an equal and oposite force upwards.