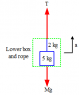
- #1
Owen443
- 3
- 0
Homework Statement
Two masses are connected by a heavy uniform rope (mass = 4 kg) and a upward force of 200N (Fa) is applied to the block on top; essentially the two masses and the rope are pulled up vertically. The mass on top (m1) weighs 6 kg, the mass on the bottom (m2) weighs 5 kg.
200 N
∧
|
m1
|
| ← 4.0 kg rope
|
m2
Find the tension at the top and middle of the heavy rope.
Homework Equations
Newton's Second Law, Fnet = ma
Force of gravity, mg
The Attempt at a Solution
I found the acceleration of the whole system:
Fnet = ma
Fg + Fa = (6+4+5)(a)
a = 3.52 m/s^2 [upwards]
So for the top of the rope I figured that the tension should be supporting the weight of the the mass below it, Fg = mg = (4+5)(9.81), but I also know that since the system is accelerating upwards the tension should be greater, so:
Fnet = Force pulling the rope up + Force of gravity + Tension = (mass of rope + mass of m2)(g)
But I'm not really sure if the magnitude of the force pulling the rope up is 200N, and how I would find it if it isn't.
I have the same problem considering the tension in the middle
Here's my Fnet for that:
Fnet = Tension pulling it up + Tension pulling it down + Fg = (mass of half the rope + mass of m2)(a)
I think I have just a big lack of understanding of tension and I'm confused about what to do... any help /clarification about what path I should take would be greatly appreciated :)