How Do You Determine Net Charge Through a Wire Over Time?

  • Thread starter Thread starter snoggerT
  • Start date Start date
  • Tags Tags
    Charge Net Wire
snoggerT
Messages
183
Reaction score
0
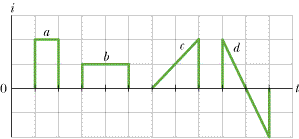
The figure below shows plots of the current i through a certain cross section of a wire over four different time periods. Rank the periods according to the net charge that passes through the cross section during the period, greatest first. (Use only the symbols > or =, for example a>b=c>d.)
hrw7_26-16.gif




i=dq/dt



The Attempt at a Solution



- I'm really not sure how to start this problem. I tried taking the charge and dividing it by the time for each one, but that didn't work. Would you have to do the integrals for them? Seems like this should be a very simple problem.
 
Physics news on Phys.org
Sure. Integrate current over time. That's charge.
 

Thread 'Direction of the magnetic field of an oscillating charge'

Hello everyone, I’m considering a point charge q that oscillates harmonically about the origin along the z-axis, e.g. $$z_{q}(t)= A\sin(wt)$$ In a strongly simplified / quasi-instantaneous approximation I ignore retardation and take the electric field at the position ##r=(x,y,z)## simply to be the “Coulomb field at the charge’s instantaneous position”: $$E(r,t)=\frac{q}{4\pi\varepsilon_{0}}\frac{r-r_{q}(t)}{||r-r_{q}(t)||^{3}}$$ with $$r_{q}(t)=(0,0,z_{q}(t))$$ (I’m aware this isn’t...
View full post »

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Similar threads

Einstein Velocity Addition for a Moving Charge in a Wire
Replies
1
Views
1K
I The vector math of relative motion of wire-loop & bar magnet
Replies
1
Views
2K
What factors determine wattage of electrons flowing through a wire?
Replies
8
Views
1K
B How is surface charge accumulated?
Replies
36
Views
6K
Charge passing through a cross section for a time varying current
Replies
2
Views
4K
Net charge contained by a cube in a region with a non-uniform E field
Replies
3
Views
3K
How Do You Calculate Wire Extension Under Sudden Loads?
Replies
15
Views
1K
How Is Linear Charge Distribution a Realistic Model in Capacitor Charging?
Replies
3
Views
4K
I How Does Temperature Affect Wire Tension at Constant Length?
Replies
4
Views
2K
Is Zero Electric Field on a Closed Surface Indicative of No Net Charge?
Replies
5
Views
6K

Hot Threads

Recent Insights

Back
Top