Physics_tryhard
- 1
- 0
I understand that this has been answered, but I can't follow it. My apologies, physics is a realm I want to understand but it doesn't come naturally and I have no High school physics background just 1st yr Engineering physics. (passed with supps.)
A particle is projected vertically upward in a constant gravitational field with an initial speed v0 . Show that if there is a retarding force proportional to the square of the instantaneous speed, the speed of the particle when it returns to the initial position is
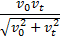
N. 2nd Law
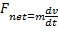
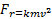
[/B]
I understand that if we first solve for the way up the boundary limit for the start is v0 and at the top acceleration must be zero which is equivalent tothe equation is
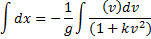
With boundary conditions of v0 and
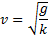 (I think...)
(I think...)
once I intergrate this that gives me the initial condition for the way down, right?
intergrating
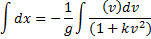
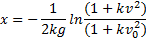
do I * by exp. to remove the ln?
e^x=e^(-1/2kg)(1+kv^2)/(1+kv0^2)
I don't think my boundary conditions are correct...
my point is what do I do from here?
A particle is projected vertically upward in a constant gravitational field with an initial speed v0 . Show that if there is a retarding force proportional to the square of the instantaneous speed, the speed of the particle when it returns to the initial position is
Homework Equations
N. 2nd Law
[/B]
The Attempt at a Solution
I understand that if we first solve for the way up the boundary limit for the start is v0 and at the top acceleration must be zero which is equivalent tothe equation is
With boundary conditions of v0 and
once I intergrate this that gives me the initial condition for the way down, right?
intergrating
do I * by exp. to remove the ln?
e^x=e^(-1/2kg)(1+kv^2)/(1+kv0^2)
I don't think my boundary conditions are correct...
my point is what do I do from here?