- #1
Ben S
- 7
- 4
I recently put together a simple 2D gravity simulator and I'd like to get some feedback or suggestions you may have for future updates. I'm planning to make a 3D version and improve the animation (framerate, realism, etc).
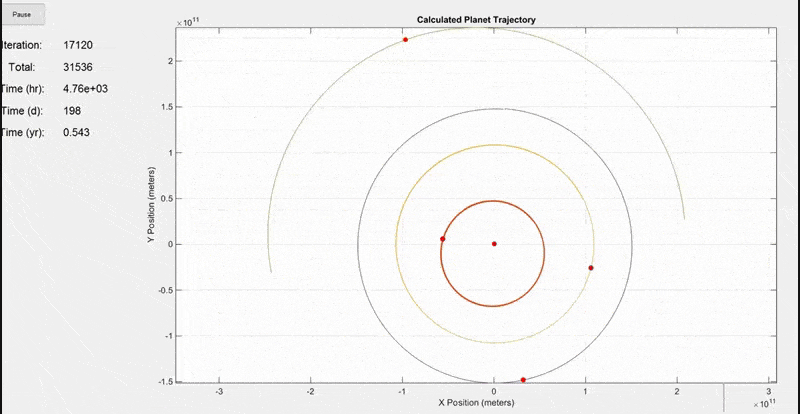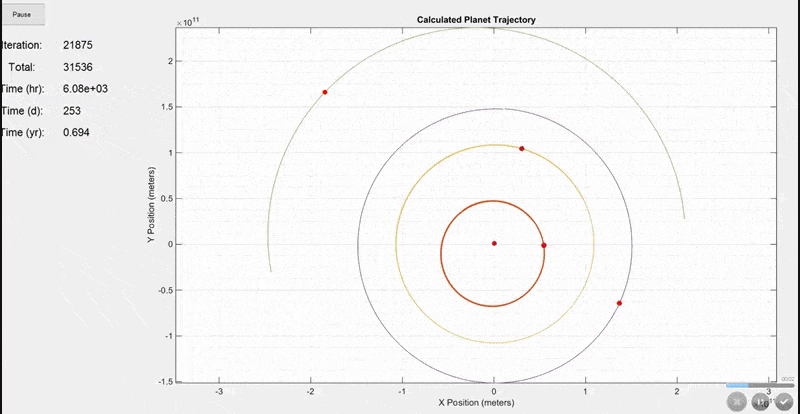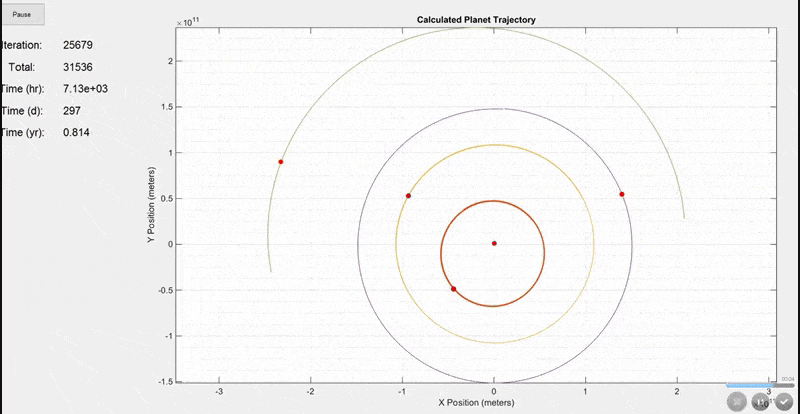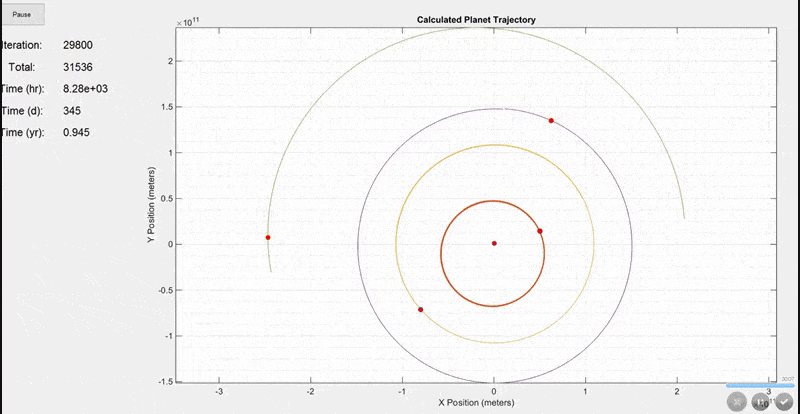
This first simulation includes the Sun, Mercury, Venus, Earth, and Mars. The initial positions and velocities were taken from NASA's JPL site. Notice how the Earth's orbit on the purple line is ~365 days shown by the time display on the left. Planets are not to scale in this model because they would be too small to see.
The inputs for the above simulation are shown below.

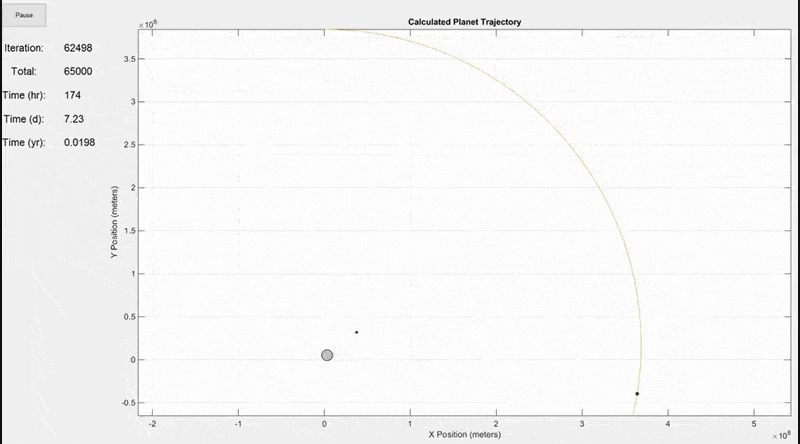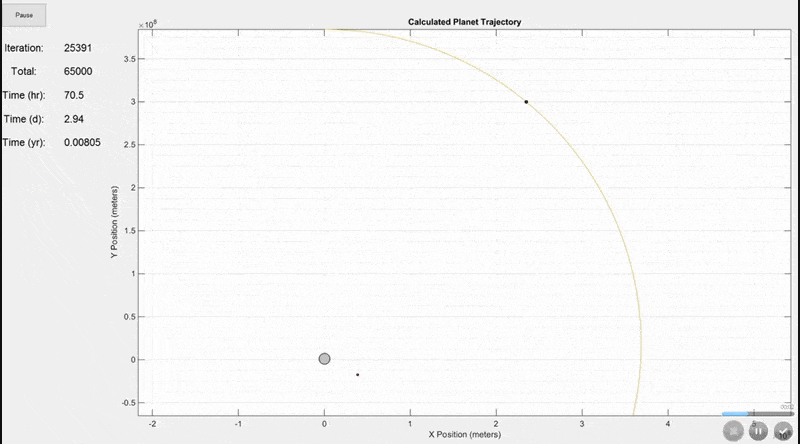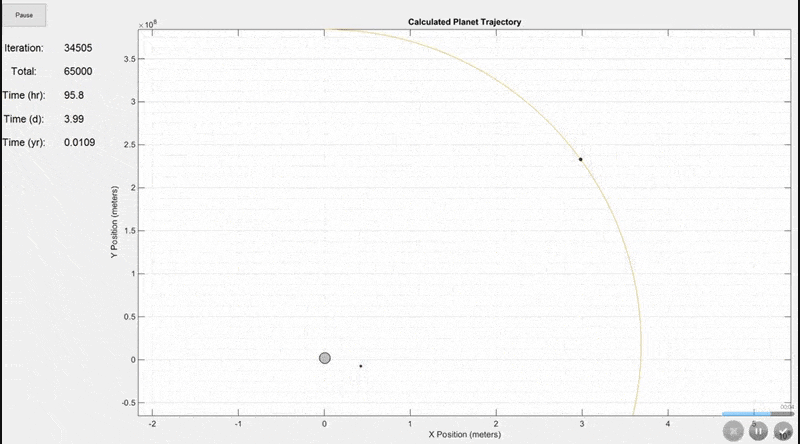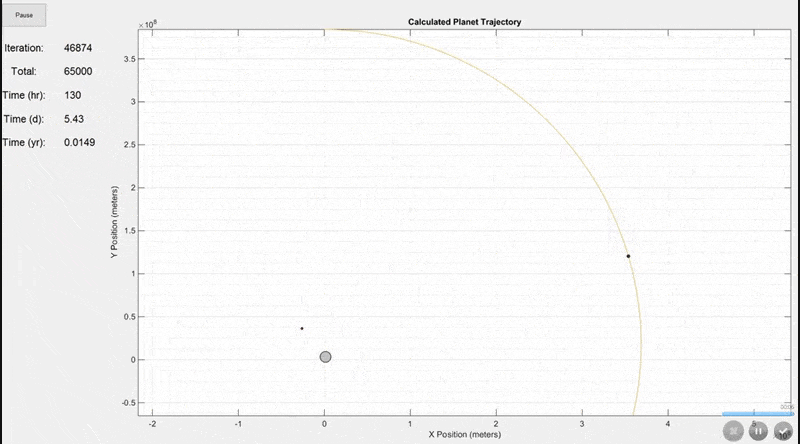
There are actually more inputs than this, but these are the most important ones. Additional inputs include the animation speed, viewing area (whether to include the full trajectory of every mass on the screen or to constantly update the viewing area size as shown in the final gif below), trajectory line visibility, and whether to show actual planet size or scaled up sizes for visibility.This simulation shows the Earth (largest grey circle), the Moon (following the yellow line), and a GSO satellite which orbits at the same rate as the Earth rotates. The simulation period is 7 days. The Earth and Moon are to scale, but the satellite size was increased so that it would be visible.
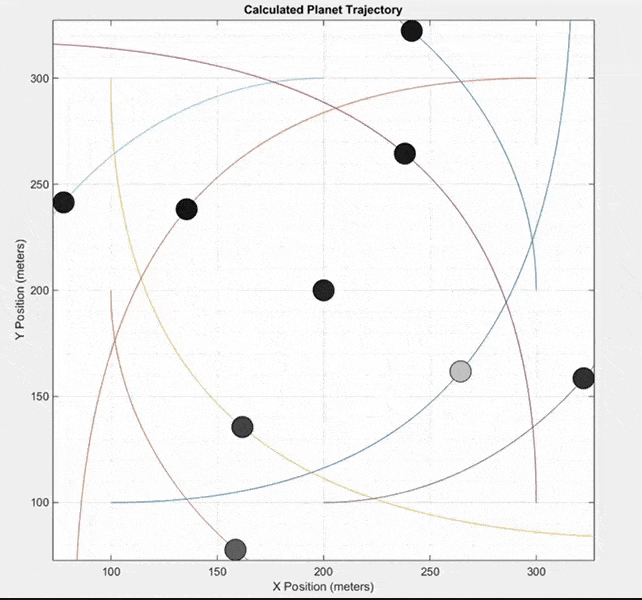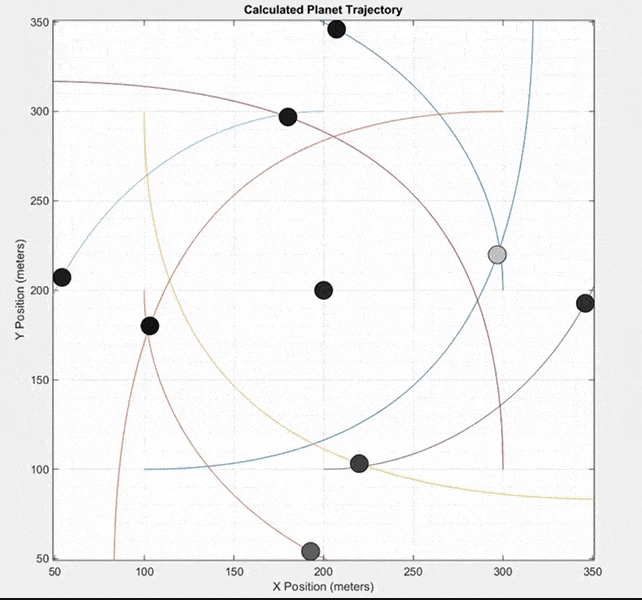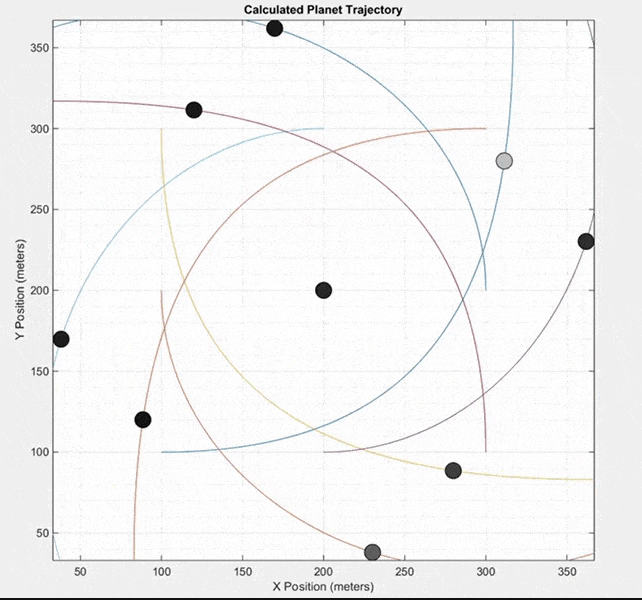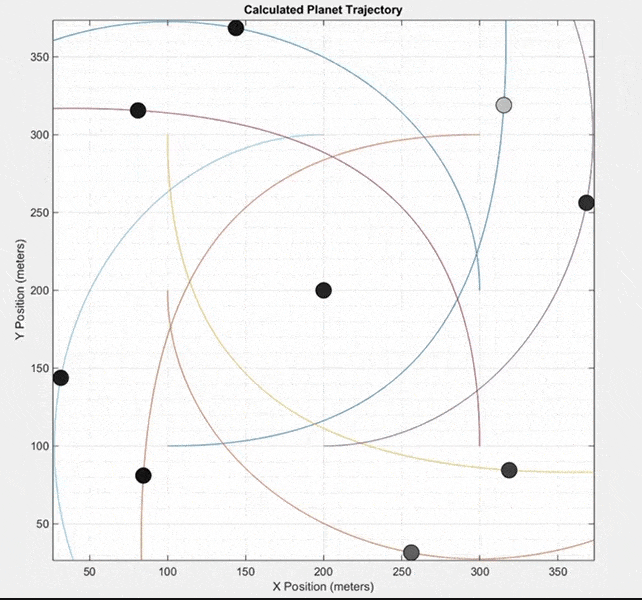
 This final simulation does not model a real system of planets like the two previous simulations. Instead, it starts with nine masses at equal distances from each other. All masses except the center mass are given an initial velocity in a counterclockwise direction around the center mass. It can produce some interesting patterns.
This final simulation does not model a real system of planets like the two previous simulations. Instead, it starts with nine masses at equal distances from each other. All masses except the center mass are given an initial velocity in a counterclockwise direction around the center mass. It can produce some interesting patterns.
 How it works
How it works
Variables are defined for the initial position (x and y), initial velocity (x and y), mass, and radius. For each planet, the acceleration vectors due to all other planets are calculated in the x and y directions using Newton's law of universal gravitation. Given a small time step, the change in velocity and position for each planet can be found using kinematic equations. I assumed the acceleration was nearly constant over the small time step. With this, the program outputs the position, velocity, and acceleration of every planet at distinct time steps over some period of time. The program is written in MATLAB.
Future work
https://www.dropbox.com/sh/q7pz43cmpxx9a48/AAA_zboKGLaH3XZ-crl_JRsma?dl=1
This first simulation includes the Sun, Mercury, Venus, Earth, and Mars. The initial positions and velocities were taken from NASA's JPL site. Notice how the Earth's orbit on the purple line is ~365 days shown by the time display on the left. Planets are not to scale in this model because they would be too small to see.
The inputs for the above simulation are shown below.
There are actually more inputs than this, but these are the most important ones. Additional inputs include the animation speed, viewing area (whether to include the full trajectory of every mass on the screen or to constantly update the viewing area size as shown in the final gif below), trajectory line visibility, and whether to show actual planet size or scaled up sizes for visibility.This simulation shows the Earth (largest grey circle), the Moon (following the yellow line), and a GSO satellite which orbits at the same rate as the Earth rotates. The simulation period is 7 days. The Earth and Moon are to scale, but the satellite size was increased so that it would be visible.
Variables are defined for the initial position (x and y), initial velocity (x and y), mass, and radius. For each planet, the acceleration vectors due to all other planets are calculated in the x and y directions using Newton's law of universal gravitation. Given a small time step, the change in velocity and position for each planet can be found using kinematic equations. I assumed the acceleration was nearly constant over the small time step. With this, the program outputs the position, velocity, and acceleration of every planet at distinct time steps over some period of time. The program is written in MATLAB.
Future work
- Improve animation frame rate
- Convert to 3D
- Apply modern gravitational theories like general relativity
https://www.dropbox.com/sh/q7pz43cmpxx9a48/AAA_zboKGLaH3XZ-crl_JRsma?dl=1
Last edited: