meganw
- 96
- 0
[a]1. Homework Statement [/b]
The block shown in Fig. 5-27 lies on a smooth plane tilted at an angle = 25.5° to the horizontal, with µk = 0.17.
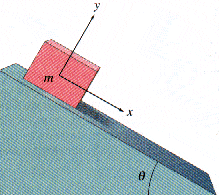
Figure 5-27
(a) Determine the acceleration of the block as it slides down the plane.
________ m/s2 (down the plane)
(b) If the block starts from rest 9.50 m up the plane from its base, what will be the block's speed when it reaches the bottom of the incline?
_________ m/s
F=m(a)
Ff=Mk(N)
[c]3. The Attempt at a Solution [/b]
I drew a Vector Diagram so that gravity was pointing directly downward from the box, so that means that the Fg vector is at an angle of -64.5 from the Horizontal, (or 25.5 degrees from the Y axis, whichever you prefer!), and then so Fg has horizontal and Vertical components.
Fy(net)=m(a)=Fa+Fgx-Ff
Ff=.17(Fnormal)
? I'm very confused..it seems like I need to know the mass to solve the problem, but the other half of me doesn't even know where to begin.
The block shown in Fig. 5-27 lies on a smooth plane tilted at an angle = 25.5° to the horizontal, with µk = 0.17.
Figure 5-27
(a) Determine the acceleration of the block as it slides down the plane.
________ m/s2 (down the plane)
(b) If the block starts from rest 9.50 m up the plane from its base, what will be the block's speed when it reaches the bottom of the incline?
_________ m/s
Homework Equations
F=m(a)
Ff=Mk(N)
[c]3. The Attempt at a Solution [/b]
I drew a Vector Diagram so that gravity was pointing directly downward from the box, so that means that the Fg vector is at an angle of -64.5 from the Horizontal, (or 25.5 degrees from the Y axis, whichever you prefer!), and then so Fg has horizontal and Vertical components.
Fy(net)=m(a)=Fa+Fgx-Ff
Ff=.17(Fnormal)
? I'm very confused..it seems like I need to know the mass to solve the problem, but the other half of me doesn't even know where to begin.
Last edited: