Jhenrique
- 676
- 4
Look this relationship:
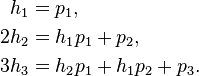
http://en.wikipedia.org/wiki/Newton's_identities#Related_identities
If I isolate the variable p, I'll have:
##p_1 = 1h_1##
##p_2 = 2h_2-h_1p_1##
##p_3 = 3h_3-h_2p_1-h_1p_2##
So, my question is: BTW, would be true that:
##p_1 = 1h_1##
##p_2 = 2h_2+h_1p_1##
##p_3 = 3h_3+h_2p_1+h_1p_2##
?
EDIT: I'm asking because with base in other formulas seems that there is some symmetry between the signals...
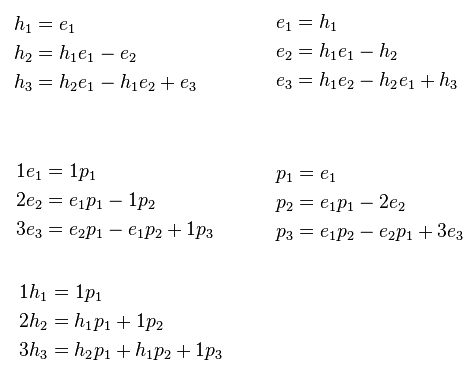
http://en.wikipedia.org/wiki/Newton's_identities#Related_identities
If I isolate the variable p, I'll have:
##p_1 = 1h_1##
##p_2 = 2h_2-h_1p_1##
##p_3 = 3h_3-h_2p_1-h_1p_2##
So, my question is: BTW, would be true that:
##p_1 = 1h_1##
##p_2 = 2h_2+h_1p_1##
##p_3 = 3h_3+h_2p_1+h_1p_2##
?
EDIT: I'm asking because with base in other formulas seems that there is some symmetry between the signals...
Last edited: