Newton's Laws; ramps and pulleys

[glacialis]

Homework Statement

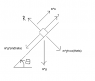
http://img201.imageshack.us/img201/6315/diagramyk1.gif
-Assuming the system is frictionless, find m₂ when it is accelerating down the ramp at 3.4 m/s₂.

Homework Equations

-... F = ma?

The Attempt at a Solution

-In this problem, I tried tilting the axis so the sliding-down part aligned with the y-axis and the m₁ part on the x-axis. Then, I thought of using the components to the F_w, to figure out the Tension on the rope for the m₂ side (which, I guessed, to be m₂a.).
I couldn't figure out what to make the Tension equal to, because m₂gcos(\theta) wasn't coming out the same as 3.4*m₂.

...I then realized I was quite retarded at physics (I'm being perfectly honest, now.) and needed help.

 

[ank_gl]

did you make the free body diagram?

 

[glacialis]

oh, sorry! I forgot to attach it... >_<;;;

http://img297.imageshack.us/img297/3359/diagram2im0.gif

I suppose what confuses me is the fact that they're on ramps; I don't know how/where to draw the gravity part.

(apologies if this is frustrating for you. I'm just really bad at physics.)

 

[ank_gl]

nooooooooooo
this is what a free body diagram for such a situation looks like.
now make the other one. write the appropriate equation ie. Fnet = m*a.
eliminate T from both the equations. you have "a", find "m" and show us what you got. ok??

 

[andrevdh]

The weight acts at the centre of gravity (mass) of the block.

 

[ank_gl]

i guess OP is asking the direction of gravitational force andrevdh

 

[glacialis]

(well, my retardation may have reached a new low.)

I figured out how to do the free-body diagram right this time, and got:

http://img254.imageshack.us/img254/5139/diagramca9.gif

\SigmaF_x = m₂gsin\alpha - T = m₂a.
and
\SigmaF_x = T- m₁gsin\beta = m₁a.

so if I solve for T it would be m₁a + m₁gsin\beta, and substitute that into the first equation to figure out m₂a.

with grouping like terms, plugging in numbers, solving, &c, I got 11.0 kg.

...would that be right?

(and a big thank you for the help!)

 

[ank_gl]

i didnt calculate the values, but the method you described, answer should be alright.