No Limits of Integration for Electric Field Integral?

[member 731016]

Homework Statement

This is a more concise version of my 'Electric Field of a Uniform Ring of Charge' thread that I posted yesterday and made a typo.

Relevant Equations

Continuous charge distribution formula

For this problem,

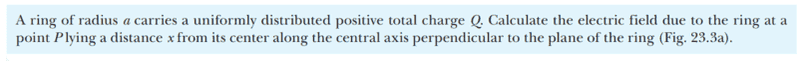
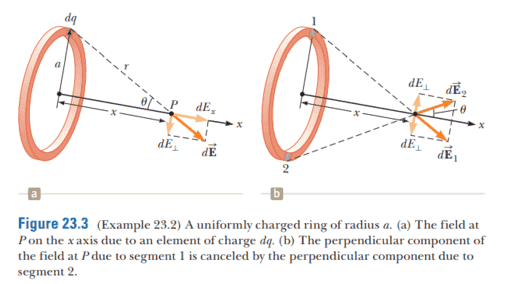
The solution is,

However, why have they not included limits of integration? I think this is because all the small charge elements dq across the ring add up to Q.

However, how would you solve this problem with limits of integration?

Many thanks!

 

[kuruman]

You can assume a uniform linear charge density on the ring, $\lambda=\dfrac{Q}{2\pi a}.$ Then an arc element $ds$ at polar angle $\phi$ in the plane of the ring subtends angle $d\phi$ so that $ds=a d\phi$. The charge on that element is $dq=\lambda ds=\lambda a d\phi$ so that when you integrate going around the ring once, you have $$\int dq=\int_0^{2\pi}\lambda a d\phi=2\pi a\lambda=2\pi a\frac{Q}{2\pi a}=Q$$Does this answer your question?

 

[member 731016]

You can assume a uniform linear charge density on the ring, $\lambda=\dfrac{Q}{2\pi a}.$ Then an arc element $ds$ at polar angle $\phi$ in the plane of the ring subtends angle $d\phi$ so that $ds=a d\phi$. The charge on that element is $dq=\lambda ds=\lambda a d\phi$ so that when you integrate going around the ring once, you have $$\int dq=\int_0^{2\pi}\lambda a d\phi=2\pi a\lambda=2\pi a\frac{Q}{2\pi a}=Q$$Does this answer your question?

Thanks for your answer @kuruman, I think that answers my question for now!

 

[member 731016]

You can assume a uniform linear charge density on the ring, $\lambda=\dfrac{Q}{2\pi a}.$ Then an arc element $ds$ at polar angle $\phi$ in the plane of the ring subtends angle $d\phi$ so that $ds=a d\phi$. The charge on that element is $dq=\lambda ds=\lambda a d\phi$ so that when you integrate going around the ring once, you have $$\int dq=\int_0^{2\pi}\lambda a d\phi=2\pi a\lambda=2\pi a\frac{Q}{2\pi a}=Q$$Does this answer your question?

Sorry @kuruman, why are you allowed to use the linear charge density, because doesn't the ring have a width too?

Are you assuming that x >> width, so the width is negligible?

Many thanks!

 

[kuruman]

Sorry @kuruman, why are you allowed to use the linear charge density, because doesn't the ring have a width too?

No, it does not have a width because the calculation assumes that it is a "thin" ring which means zero width. If it has a width, say it is a washer of inner radius $a$ and outer radius $b$, then you have to do a different calculation and also integrate over $r$ from $a$ to $b$. That's a different homework problem.

 

[member 731016]

Thanks for helping me @kuruman!