- #1
willow16v
- 12
- 0
Hi,
I would be grateful of any advice on how to solve the problem below.
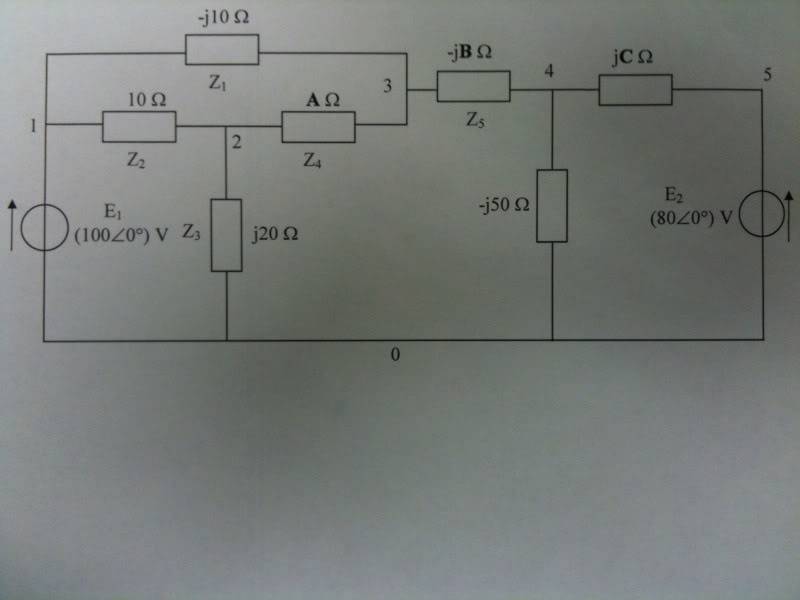
My aim is to find the voltages at nodes 2, 3, and 4, by means nodal analysis and thus creating simultaneous equations and solving them using matricies or matrix in order to prove that these theories work.
I understand kirchhoffs law etc however its the complex numbers that are throwing me when working out the equations at each node.
, e.g multiplying and dividing by j etc.
I have tried for weeks now and it seems i am beaten yet again on my failure of rearranging algebra.
Any help would be great.
A=60 B=15 C=153
See diagram Below.
Cheers Chris
I would be grateful of any advice on how to solve the problem below.
My aim is to find the voltages at nodes 2, 3, and 4, by means nodal analysis and thus creating simultaneous equations and solving them using matricies or matrix in order to prove that these theories work.
I understand kirchhoffs law etc however its the complex numbers that are throwing me when working out the equations at each node.
, e.g multiplying and dividing by j etc.
I have tried for weeks now and it seems i am beaten yet again on my failure of rearranging algebra.
Any help would be great.
A=60 B=15 C=153
See diagram Below.
Cheers Chris