Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading the book "An Introduction to Rings and Modules with K-theory in View" by A.J. Berrick and M.E. Keating ... ...
I am currently focused on Chapter 3; Noetherian Rings and Polynomial Rings.
I need someone to help me to fully understand the maximal condition for modules and its implications ...
On page 111, Berrick and Keating state the following:
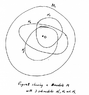
"The module M is said to satisfy the maximum condition if any nonempty set of submodules of M has a maximal member (with respect to inclusion) "It seems to me that this definition, when it is satisfied, means that all the submodules of M must be in a chain of inclusions ... so we cannot have a situation like that depicted in Figure 1 below:
 Can someone confirm that my basic understanding of the implication of the definition mentioned above is correct ... ... and/or ... ... give a simple explanation of the maximal condition ...
Can someone confirm that my basic understanding of the implication of the definition mentioned above is correct ... ... and/or ... ... give a simple explanation of the maximal condition ...
Help will be appreciated ...
Peter
==================================================
*** EDIT ***
Just reflecting a bit on this matter ... ...Maybe the maximal condition means that for any collection of submodules IF one can arrange a subset into an ascending chain of inclusions then that chain will have a maximal member ... ... ?
Mind you if that is true ... then you can have several maximal members ...
Hope someone can clarify this issue for me ...
Peter
I am currently focused on Chapter 3; Noetherian Rings and Polynomial Rings.
I need someone to help me to fully understand the maximal condition for modules and its implications ...
On page 111, Berrick and Keating state the following:
"The module M is said to satisfy the maximum condition if any nonempty set of submodules of M has a maximal member (with respect to inclusion) "It seems to me that this definition, when it is satisfied, means that all the submodules of M must be in a chain of inclusions ... so we cannot have a situation like that depicted in Figure 1 below:
Help will be appreciated ...
Peter
==================================================
*** EDIT ***
Just reflecting a bit on this matter ... ...Maybe the maximal condition means that for any collection of submodules IF one can arrange a subset into an ascending chain of inclusions then that chain will have a maximal member ... ... ?
Mind you if that is true ... then you can have several maximal members ...
Hope someone can clarify this issue for me ...
Peter