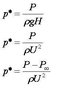Nondimensionlization of Pressure

[hanson]

Hi all.
When I read through text in fluid mechanics, I see various ways of non-dimensionlising the pressure. (Please see the figure)

To me, non-dimensionlize a quantity is to make it of order unity to facilitate the mathematical processes needed afterwards.
So, I can understand why density*gravity*H is used as a characteristic scale to non-dimensionlize the pressure since it is the maximum hydrostatic pressure.

But I don't understand why density*U^2 is used to non-dimensionalize the pressure as well? In what situation is this nondimensionlization valid?

What about the P(infinity), what is it?

 

[FredGarvin]

The second two numbers are actually referred to as the Euler number (ref http://en.wikipedia.org/wiki/Euler_number_(physics)). It is another dimensionless number. I don't really use it myself (I don't need to stray too much from the Reynolds number), but my handy, dandy fluids reference lists it as a useful number when dealing with pressure differences, such as in cavitation analyses. Actually, the third version you show is what is listed for a cavitation analysis (without a .5 factor) where the P is actually a reference pressure and the $$P_{\infinity}$$ is the vapor pressure of the working fluid.

Omega Engineering has a neat poster you can request that has a ton of dimensionless numbers and their uses. You can also look at a lot of them here on Wiki: http://en.wikipedia.org/wiki/Category:Dimensionless_numbers

 

[hanson]

The second two numbers are actually referred to as the Euler number (ref http://en.wikipedia.org/wiki/Euler_number_(physics)). It is another dimensionless number. I don't really use it myself (I don't need to stray too much from the Reynolds number), but my handy, dandy fluids reference lists it as a useful number when dealing with pressure differences, such as in cavitation analyses. Actually, the third version you show is what is listed for a cavitation analysis (without a .5 factor) where the P is actually a reference pressure and the $$P_{\infinity}$$ is the vapor pressure of the working fluid.

Omega Engineering has a neat poster you can request that has a ton of dimensionless numbers and their uses. You can also look at a lot of them here on Wiki: http://en.wikipedia.org/wiki/Category:Dimensionless_numbers

Thanks. But why density * U^2 is used to non-dimensionlize the pressure? I don't understand the rationale behind...