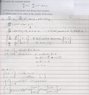Nonlinear system phase portraits

[schmiggy]

Homework Statement

See attached image

Homework Equations

Classification of critical points chart (unless you remember it)

The Attempt at a Solution

See attached.

Now, I'm not entirely sure what exactly I'm doing. With linear systems, the goal is to find the eigenvectors, eigenvalues and thus the general solution. Using the general solution you can then derive the attributes of the phase portrait for that particular system to aid in sketching (such as behaviour as t -> +- infinity). Is that what I'm supposed to be doing here?

So basically, taking the critical points and substituting them into the matrix and then finding the eigenvalues and vectors for the respective matrix? Then do the same again for the next critical point? Is the goal to end up with as many general solutions as there are critical points and then combine them into one sketch?

I'm not really sure what the "let X=x, Y=y" is for either, I was trying to follow an example in my lecture notes on how to linearise the system but that's where it stops - thus why I thought the goal might be to linearise the system and then find the respective general system (for each critical point).

Also, I feel like I've done something wrong making the matrix and made up some pretend maths to get my lambda for the (0,0) critical point. What a mess! Any direction would be appreciated, thanks :)

 

[Rikardus]

You have a first order nonlinear system, which can be written as X' = f(X), where X is a vector.
In such systems, the phase portrait around a hyperbolic equilibrium point (an equilibrium point X* such that the real part of every eigenvalue of Df(X*) is nonzero) is the same as the phase portrait of the linear system X' = Df(X*).X, in a neighbourhood of X*.

This means that in a vicinity of X* the phase portraits are the same, and you can deduce the stability by analysing the linear system.

Remark: Df(X*) is the jacobian matrix evaluated at the equilibrium point X*.