Object Suspended by Two Strings (Tension Problem)

[A R]

Homework Statement

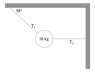
An object with a mass of 18 kg is suspended from 2 cables as shown in the below diagram. The tensions in the cables are T₁ and T₂.
a) Draw a free-body diagram for the object. (already solved)
b) Find the tension in both ropes, T₁ and T₂. (already solved)
c) If string 2 were cut, how would its FBD change at that instant? Sketch a new one. (already solved)
d) What would be the magnitude and direction of the object's acceleration at that instant? (already solved)
e) Would T₁ be different in part (b) than in part (d)? If so, what is its new value?

2. Homework Equations
ΣF = ma_x = w sinθ (w is weight)

The Attempt at a Solution

b) T₁ = mg/sinθ = (18*9.8)/sin58 = 208 N
T_1,x = T₂ = T₁cosθ = 208 (cos58) = 110 N

d) a_x = g⋅sinθ = 9.8 (sin58) = 8.31 m/s²

Now the real question...
e) Yes, T₁ = mg⋅sinθ = (18)(9.8)(sin58) = 149.6 N

Friend says that it will be mg⋅cosθ = 93.5 N

Please help out with this question! I know it may be simple but I'm having trouble understanding how T₁ changes.

 

[mfb]

Imagine the extreme case of 90° or an angle very close to 0°. What do the two different results give, and which one is realistic?