Sujith Sizon
Gold Member
- 7
- 0
Q) two identical smooth balls are projected from points O and A on the horizontal ground with the same speed of projection the angle of projection in each case is 30 The distance between O and A is 100m . The balls collide in mid air And return to their respective points of projection if coefficient of restitution is 0.7 find the speed of projection of either ball (m/s) correct to nearest integer ?
Question figure
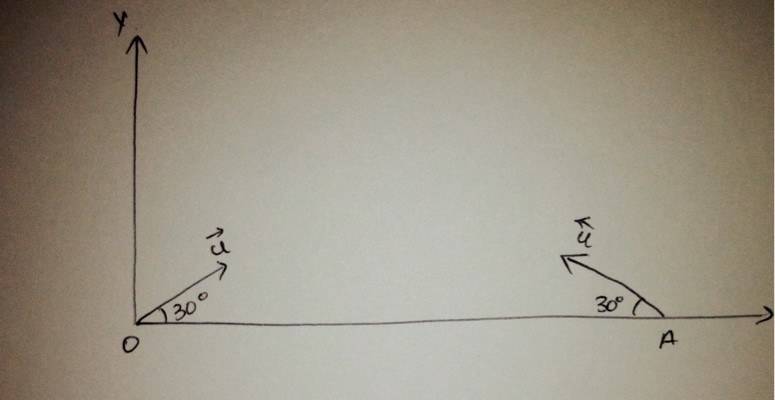
My Attempt :
Taking ##y## as the height from the ground to the point where the masses collide and ##\alpha## as the angle made by the final velocity vector with the horizontal .
Using projectile equation ie : ##y=x\tan\theta\left[1-\frac{x}{R}\right]##
For the case when it is projected and reaches a height ##y##
##y=\frac{50}{\sqrt{3}}\left[1-\frac{50\times 20}{\sqrt{3}u^{2}}\right]##
For its return path considering a projectile motion from height ##y## with velocity vector making an angle ##\alpha## with the horizontal we get
##y=50\tan\alpha\left[1-\frac{50\times g}{v^{2}\sin2\alpha}\right]##
The from coefficient of restitution formula we get
##e\rightarrow0.7=\frac{2v\cos\alpha}{2u\cos30}##
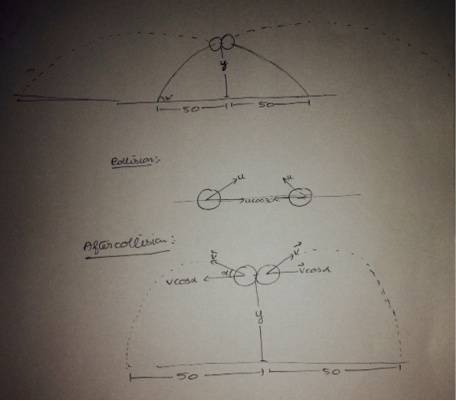
Now assuming that my procedure so far is appropriate i need one more equation so that i can find ##u## and ##v##
SOLVED (thanks to TSny)
Conserving momentum along tangential component we will have
##2mu\sin30 = 2mv\sin\alpha##
Question figure
My Attempt :
Taking ##y## as the height from the ground to the point where the masses collide and ##\alpha## as the angle made by the final velocity vector with the horizontal .
Using projectile equation ie : ##y=x\tan\theta\left[1-\frac{x}{R}\right]##
For the case when it is projected and reaches a height ##y##
##y=\frac{50}{\sqrt{3}}\left[1-\frac{50\times 20}{\sqrt{3}u^{2}}\right]##
For its return path considering a projectile motion from height ##y## with velocity vector making an angle ##\alpha## with the horizontal we get
##y=50\tan\alpha\left[1-\frac{50\times g}{v^{2}\sin2\alpha}\right]##
The from coefficient of restitution formula we get
##e\rightarrow0.7=\frac{2v\cos\alpha}{2u\cos30}##
Now assuming that my procedure so far is appropriate i need one more equation so that i can find ##u## and ##v##
SOLVED (thanks to TSny)
Conserving momentum along tangential component we will have
##2mu\sin30 = 2mv\sin\alpha##
Last edited: