Oblique Impact of a smooth sphere against a fixed plane

[andyrk]

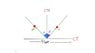
A sphere of mass 'm' collides with a fixed plane with initial speed 'u' at an angle 'α'(alpha). The sphere rebounds with speed 'v' at an angle 'β' with the normal. The plane being fixed remains at rest.
We applied Newton's Experimental law( along the common normal(CN)
The equation after applying Newton's Experimental law along CN becomes:
V_seperation along CN =eV_approach
where 'e' is the coefficient of restitution.
On the other hand, we applied Conservation of Momentum along the Common Tangent(CT) as there is no force along CT.
So after applying conservation of momentum along CT we get the following equation:
(u)(sinα)=(v)(sinβ)
But we could have also conserved momentum along CN as there is no net force acting along the CN. This is because during collision,
N(Normal Reaction)=mg(weight of the sphere)
But since this is not done so it means that there is a net force along CN. What is that force? Or rather, what is that NET force? I think it is Impulse but why does the Impulsive force become greater than the weight of the object at the time of collision? Also, how does that impulsive force arise? Is it because of the normal reactions that the ball and the floor impart on each other when the ball collides with the floor or and Impulsive force is a completely different force just like Normal Reaction? Since the ball bounces back there has to be a net vertical force in the upward direction at the time of colliding. That is impulse..but why? Also, why is it specifically mentioned that the sphere is smooth? What would happen if it won't be smooth?Please reply fast!

 

[haruspex]

First, in the statement of the problem there is no mention of gravity or orientation of the plane.
Secondly, since the duration of the impact is presumably very short, we are not really dealing with forces here, just impulses. (Yes, there are forces involved, but we've no idea of the magnitude.) The plane exerts an impulse on the sphere. You can use conservation of momentum to calculate it, but there's no point unless you are asked to calculate it.
Thirdly, "N(Normal Reaction)=mg(weight of the sphere) " applies in statics, i.e. a body at rest on a surface under gravity.
Smoothness is required because a frictional contact would create a tangential impulse, imparting spin to the sphere and reducing its tangential speed.

 

[andyrk]

So if I correctly inferred from what you wrote you mean that had the floor been rough we would not have been able to conserve momentum even along CT as there would be a frictional impulse? And just confirming, to calculate the impulse imparted on the ball we just find the change in momentum after and before the collision and divide it by the time of contact for collision, right? Thanks for the help :)And oh, yup there is no mention of gravity or orientation of the plane it is just a smooth plane which can be assumed to be surface of Earth so that's the orientation.

 

[haruspex]

So if I correctly inferred from what you wrote you mean that had the floor been rough we would not have been able to conserve momentum even along CT as there would be a frictional impulse?

Yes.

And just confirming, to calculate the impulse imparted on the ball we just find the change in momentum after and before the collision and divide it by the time of contact for collision, right?

No, you would not divide by time. Impulse is change in momentum, no matter how long it takes. Dividing by time would give you the average force, but that's rarely interesting.

there is no mention of gravity or orientation of the plane it is just a smooth plane which can be assumed to be surface of Earth so that's the orientation.

No, unless indicated, I would assume this is in an arbitrary orientation and in the absence of gravity. But for the purposes of this question, it makes no difference - the answer is the same. The impulse is considered so short there's no time for gravity to affect anything.

 

[andyrk]

what would be the direction of tangential impulse in that case?

 

[Tanya Sharma]

what would be the direction of tangential impulse in that case?

Along the surface of the plane :)

 

[andyrk]

To the left or to the right?(According to the attachment)
I think towards left as the sphere would be moving towards the right and friction opposes motion..just wanted to confirm

 

[haruspex]

To the left or to the right?(According to the attachment)

Friction always acts to oppose relative movement of the surfaces in contact.

 

[andyrk]

Friction always acts to oppose relative movement of the surfaces in contact.

So it would be to the left right?

 

[Tanya Sharma]

To the left or to the right?(According to the attachment)
I think towards left as the sphere would be moving towards the right and friction opposes motion..just wanted to confirm

Consider only the component of velocity parallel to surface ,i.e usinα .The direction of this velocity is towards right and friction acts so as to oppose relative motion .Hence it acts towards left on the sphere .

 

[andyrk]

Thanks :)