iknowless
- 11
- 0
Homework Statement
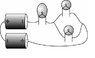
When a single round bulb of a particular kind and two batteries are connected in series, 5* 10^18 electrons pass through the bulb every second. When a single long bulb of a particular kind and two batteries are connected in series, only 2.5*10^18 electrons pass through the bulb every second, because the filament has a smaller cross section.Figure 18.68
In the circuit shown in Figure 18.68, how many electrons per second flow through the long bulb?
E is the electric field in the filament
A is the cross-sectional area of the filament
i is electron current
l is the length of the filament
n is the # of electrons per unit volume (unknown)
u is the electron mobility (unknown)
Homework Equations
Circuit 1 is the main circuit, with long bulb A, and two identical round bulbs, both labeled B.
Circuit 2 is the circuit with 1 long bulb, C.
Circuit 3 is the circuit with 1 round bulb, D
i_1=nA_auE_a=n2A_buE_b
i_2=nA_auE_c=2.5e18
i_3=nA_buE_d=5e18
2emf=l(E_a+2E_b)=E_c l=E_d l
The Attempt at a Solution
note: A_b>A_a
E_c=E_d
I am assuming that all the filaments have a length 'l.'
I have created fractions of current to produce some hopefully useful formulae.
From i_1, A_a E_a=2A_b E_b
From \frac{i_1}{i_2}, E_a i_2 =2 E_b i_3
Also, i_1=\frac{E_a i_2}{E_c}=\frac{2 E_b i_3}{E_c}
And \frac{i_2}{i_3} = \frac{A_a}{A_b}
E_a+2E_b=2E_b+E_b \frac{i_3}{i_2}=E_c
Please just give me a nudge in the right direction. Thanks!
Attachments
Last edited: