- #1
cmkluza
- 118
- 1
I'm trying to read up on some traffic flow models and I've encountered the following equation (source [pdf]):
Variables are ##t =## time, ##x =## space variable along road, ##\rho (t, x) =## density of cars, ##v(\rho ) =## velocity, ##Q = \rho \times v##
Following graphic is used to show situation:
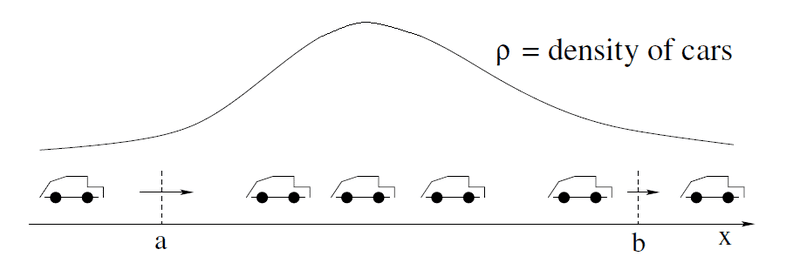
If total number of vehicles is conserved:
[tex]\frac{d}{dt} \int^b_a \rho (t, x) dx = Q_a - Q_b[/tex]
[tex]\frac{d}{dt} \int^b_a \rho (t, x) dx = \rho (t,a)v(\rho (t,a)) - \rho (t,b)v(\rho (t,b))[/tex]
What are these equations actually showing, namely the first bit (derivative of integral of density)? I'm a bit confused since I'm not too familiar with the math behind it. Ignoring numbers and math right now, what are the physical interactions described by this? That might not be worded to clearly, so what does the integral of the density with respect to distance show? What, then, does the derivative with respect to time show?
Sorry if this is asking a lot, but any help understanding this will be appreciated!
Variables are ##t =## time, ##x =## space variable along road, ##\rho (t, x) =## density of cars, ##v(\rho ) =## velocity, ##Q = \rho \times v##
Following graphic is used to show situation:
If total number of vehicles is conserved:
[tex]\frac{d}{dt} \int^b_a \rho (t, x) dx = Q_a - Q_b[/tex]
[tex]\frac{d}{dt} \int^b_a \rho (t, x) dx = \rho (t,a)v(\rho (t,a)) - \rho (t,b)v(\rho (t,b))[/tex]
What are these equations actually showing, namely the first bit (derivative of integral of density)? I'm a bit confused since I'm not too familiar with the math behind it. Ignoring numbers and math right now, what are the physical interactions described by this? That might not be worded to clearly, so what does the integral of the density with respect to distance show? What, then, does the derivative with respect to time show?
Sorry if this is asking a lot, but any help understanding this will be appreciated!