I Filling a rigid tire from a pressure regulated compressed air line

[erobz]

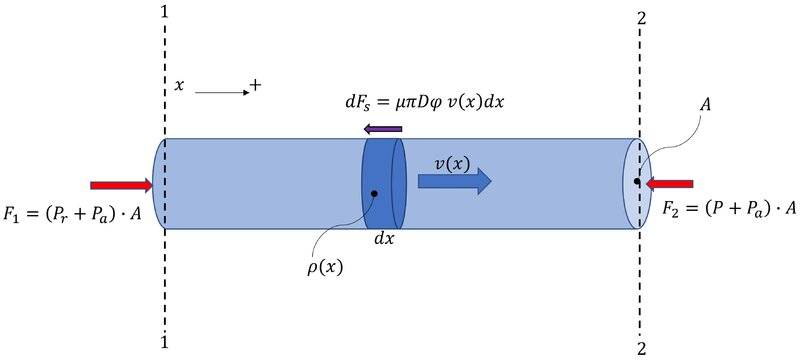
The figure below shows the new control volume that is between the regulated pressure from the tank supply $P_r$ and the tire at pressure $P$. I'm applying (1) the control volume

$$ \sum F = \frac{d}{dt} \int_{cv} \boldsymbol v \rho d V\llap{-} +\int_{cs} \boldsymbol v \rho \boldsymbol V \cdot d \boldsymbol A \tag{1} $$

$\underline{\sum F}$

Since we have from the earlier result that the Shear Force resisting the flow was porportional to the flow velocity within the variable $\tau = \varphi v$, we now have to consider the total shear force acting the control volume as integral because the velocity is varying over the length of the tube.

$$ \sum F = \left( P_r + P_a \right) A - \left( P(t) + P_a \right) A - \mu \pi D \varphi \int v(x,t) \, dx $$

Momentum Accumulation Term:

This time the only quantity that can be taken outside the integral is the cross sectional area and we can drop the vector notation.

$$ \frac{d}{dt} \int_{cv} \boldsymbol v \rho d V\llap{-} = A \frac{d}{dt} \int v(x,t) \rho (x,t) dx $$

Net Efflux of Momentum Term:

I'm considering the properties $\rho$ and $v$ as uniformily distributed across the area of the pipe at section 1 and 2.

$$ \int_{cs} \boldsymbol v \rho \boldsymbol V \cdot d \boldsymbol A = A \left( \rho_2(t) {v_2(t)}^2 - \rho_r {v_1(t)}^2 \right) $$

$$ P_r A - P(t)A - \mu \pi D \varphi \int v(x,t) \, dx = A \frac{d}{dt} \int v(x,t) \rho (x,t) dx + A \left( \rho_2(t) {v_2(t)}^2 - \rho_r {v_1(t)}^2 \right) $$

As far as I can see this is step 1.

 

[bob012345]

Instead of starting from scratch I would suggest you look at the assumptions @Chestermiller made above and start with that. Dig into what assumptions were made and why they were made. Then you can fill in the derivational details of his logical flow which was nicely laid out for you.

 

[erobz]

Instead of starting from scratch I would suggest you look at the assumptions @Chestermiller made above and start with that. Dig into what assumptions were made and why they were made. Then you can fill in the derivational details of his logical flow which was nicely laid out for you.

I haven't been able to track down the original derivation that leads to this, which is where the meat of the analysis will be.

$$\dot{m}=\frac{\rho_R\pi^2D^6}{512\mu L}(p_R-p_T)$$

I'm not sure I'm getting something here:

$$\frac{\dot{m}}{M}=\frac{V}{RT}\frac{dp_T}{dt}$$

With properties of the mass of the air inside the tire ( Temperature, Volume, Ideal Gas Constant ) fixed:

$$ P = \rho R T \implies \frac{dP}{dt} = \frac{dm}{dt} \frac{RT}{V\llap{-} } \implies \dot m = \frac{V\llap{-} }{RT} \frac{dp}{dt} $$

But that's not quite what has been written ( I suspect a typo).

$$\frac{dp_T}{dt}=k(p_R-p_T)$$

Solving the resulting differential equation is straight forward with a $u = p_R - p_T$ substitution

 

[bob012345]

I haven't been able to track down the original derivation that leads to this, which is where the meat of the analysis will be.

I'm not sure I'm getting something here:

With properties of the mass of the air inside the tire ( Temperature, Volume, Ideal Gas Constant ) fixed:

$$ P = \rho R T \implies \frac{dP}{dt} = \frac{dm}{dt} \frac{RT}{V\llap{-} } \implies \dot m = \frac{V\llap{-} }{RT} \frac{dp}{dt} $$

But that's not quite what has been written ( I suspect a typo).

$M$ is Molar mass I think and $m$ is actual mass so $\dot{m}$ is the mass flow rate. I usually write the Ideal Gas Law as $PV= nRT$ where $n$ is the number of moles. Here $n=\large \frac{m}{M}$.

 

[erobz]

$M$ is Molar mass I think and $m$ is actual mass so $\dot{m}$ is the mass flow rate. I usually write the Ideal Gas Law as $PV= nRT$ where $n$ is the number of moles. Here $n=\large \frac{m}{M}$.

Ahhh, yes. We typically used the Specific Gas Constant in engineering which that is "baked" into. I wasn't expecting the Chemist/Physicist standard.

 

[waross]

A reality check based on the capacitor analogy.
Based on charging a capacitor from a 100 Volt source.
In one time constant, the voltage will rise to approximately 63 Volts or 63%.
At the end of one time constant, there will be 37% or 37 Volts driving the charging current.
We will start expressing the percentage charge voltage as (100% minus .63%)^N N being the number of time constants.
At the end of the Second time constant: 100V - (.37^2 x 100)V = 87V
At the end of the Fifth time constant: 100V - (.37^5 x 100)V = 99.3V
For real world applications in the field, a condition is assumed to have stabilized after five time constants.
but to continue:
At the end of 10 time constants: 100V - (.37^10 x 100)V = 99.5V
At the end of 20 time constants: 100V - (.37^20 x 100)V = 9999998V

For an exact value in place of .37, use 0.36787944117144844353582058542057 the reciprocal of E the base of natural logarithms.

Yes, I have done a lot of rounding and I have ignored a lot of factors; compressibility, temperature changes, friction, changes in atmospheric pressure, tidal effect oscillation and probably other factors.
Does it matter? Yes, in some instances other factors will matter, but if the process is not terminated, a few more time constants will render the errors minute.

The question was:
Will the pressures equalize?
If one vessel is directly connected to another vessel, probably not until some other factor causes equality.
If a pressure regulating valve is used, it may depend on the design of the valve.

A random thought; A U-Tube manometer may never be exactly accurate.

Another random thought; Why does the toilet not continue to run after you flush it? Answer, the design of the control valve.

Don't get me wrong. I have nothing against a thorough investigation of all possible sources of error or effects.
I have found that a quick and dirty solution is often adequate for field work.
Much of my career has been seat of the pants engineering. Problem solving in remote locations with not resources and few instruments.
No library, just my memory of basic principles.
A bad exciter on a diesel generator in the Yukon Territory, a few miles from Lac Labarge.
Setting the frequency of a diesel generator in the Moskito Coast of Honduras with an old electric clock and a wrist watch.
I was taken across a lagoon in a dugout canoe, and then the rest of the way to the location by saddle horse.
For another generator in the Moskito Coast, I was transported by speed boat.
It had lost its residual magnetism. I was able to boot-strap the set with D cell from a flashlight.
Seat of the pants all the way.

 

[Baluncore]

Welcome to PF.

At the end of 20 time constants: 100V - (.37^20 x 100)V = 9999998V

The decimal point is important.
At the end of 20 time constants: 100 V - (.37^20 x 100) V = 99.99998 V
And two missing nines.
At the end of 20 time constants: 100 V * ( 1 - .3679^20 ) = 99.9999998 V

 

[waross]

Thank you for the correction. I suffer senior moments and brain farts.
The point is; With short time constants, PU errors become vanishingly small.
Offset errors persist, but offset errors may be caused by inaccurate measuring equipment or by hidden factors.

Tip: As the tire pressure increases, a series of pressure checks at regular intervals may be used to calculate the time constant.
One time-pressure measurement is adequate to calculate a time constant.
Multiple measurements may identify a less than perfect system.
The time factor should remain, well, constant.
One possible source of confusion is the cooling effect as the compressed air expands through the orifice of the pressure regulator, and then warms up in he heat sink of the air already in the tire.

Back to the capacitor analogy:
Consider the case where a forward biased diode is hidden in the charging circuit.
The capacitor voltage will approach the source voltage minus the forward voltage drop of the diode.
If our multiple time constant calculations are based on the capacitor voltage approaching the source voltage rather than approaching the source voltage minus the diode voltage drop, our calculated time constants will not agree.