- #1
Independent
- 39
- 15
How does one arrive at the formula 4.8?

The Lagrangian (one spatial dimension) is:
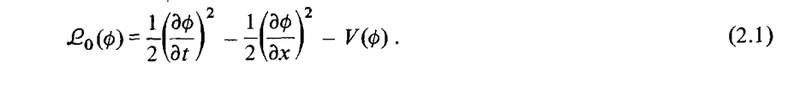
The Lagrangian (one spatial dimension) is: